Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T13:30:09.052Z Has data issue: false hasContentIssue false
  • English
  • Français

A Hitting Time Formula for the Discrete Green's Function

Part of: Graph theory

Published online by Cambridge University Press:  29 June 2015

ANDREW BEVERIDGE
ANDREW BEVERIDGE*
Affiliation:
Department of Mathematics, Statistics and Computer Science, Macalester College, 1600 Grand Avenue, St Paul, MN 55105, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The discrete Green's function (without boundary) 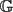$\mathbb{G}$ is a pseudo-inverse of the combinatorial Laplace operator of a graph G = (V, E). We reveal the intimate connection between Green's function and the theory of exact stopping rules for random walks on graphs. We give an elementary formula for Green's function in terms of state-to-state hitting times of the underlying graph. Namely,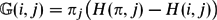$\mathbb{G}(i,j) = \pi_j \bigl( H(\pi,j) - H(i,j) \bigr),$ where πi is the stationary distribution at vertex i, H(i, j) is the expected hitting time for a random walk starting from vertex i to first reach vertex j, and H(π, j) = ∑k∈V πkH(k, j). This formula also holds for the digraph Laplace operator.

The most important characteristics of a stopping rule are its exit frequencies, which are the expected number of exits of a given vertex before the rule halts the walk. We show that Green's function is, in fact, a matrix of exit frequencies plus a rank one matrix. In the undirected case, we derive spectral formulas for Green's function and for some mixing measures arising from stopping rules. Finally, we further explore the exit frequency matrix point of view, and discuss a natural generalization of Green's function for any distribution τ defined on the vertex set of the graph.

MSC classification

Primary: 05C81: Random walks on graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 3 , May 2016 , pp. 362 - 379
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Aldous, D. and Fill, J. (accessed October 2014) Reversible Markov Chains and Random Walks on Graphs, monograph in preparation. www.stat.berkeley.edu/~aldous/RWG/book.html Google Scholar
[2] Aldous, D., Lovász, L. and Winkler, P. (1997) Mixing times for uniformly ergodic Markov chains. Stoch. Process. Appl. 71 165–185.CrossRefGoogle Scholar
[3] Beveridge, A. (2009) Centers for random walks on trees. SIAM J. Discrete Math. 23 300–318.Google Scholar
[4] Beveridge, A. and Lovász, L. (2010) Exit frequency matrices for finite Markov chains. Combin. Probab. Comput. 19 541–560.CrossRefGoogle Scholar
[5] Beveridge, A. and Wang, M. (2013) Exact mixing times for random walks on trees. Graphs Combin. 29 757–772.Google Scholar
[6] Beveridge, A. and Youngblood, J. The best mixing time for trees. Submitted. http://arxiv.org/abs/1410.5112 Google Scholar
[7] Boehnlein, E., Chin, P., Sinha, A. and Lu, L. (2014) Computing diffusion state distance using Green's function and heat kernel on graphs. In Algorithms and Models for the Web Graph: 11th International Workshop, WAW 2014 (Bonato, A., Graham, F. Chung and Prałat, P., eds), Vol. 8882 of Lecture Notes in Computer Science, Springer, pp. 79–95.CrossRefGoogle Scholar
[8] Chung, F. (1997) Spectral Graph Theory, AMS.Google Scholar
[9] Chung, F. and Yau, S.-T. (2000) Discrete Green's functions. J. Combin. Theory Ser. A 91 191–214.CrossRefGoogle Scholar
[10] Coppersmith, D., Tetali, P. and Winkler, P. (1993) Collisions among random walks on a graph. SIAM J. Discrete Math. 6 363–374.CrossRefGoogle Scholar
[11] Ellis, R. Discrete Green's functions for products of regular graphs. arXiv:math/0309080 Google Scholar
[12] Li, Y. and Zhang, Z. L. (2011) Random walks on digraphs, the generalized digraph Laplacian and the degree of asymmetry. In Algorithms and Models for the Web Graph: 7th International Workshop, WAW 2010 (Kumar, R. and Sivakumar, D., eds), Vol. 6516 of Lecture Notes in Computer Science, Springer, pp. 74–85.Google Scholar
[13] Lovász, L. (1996) Random walks on graphs: A survey. In Combinatorics: Paul Erdős is Eighty, Vol II (Miklós, D., Sós, V. T. and Szőnyi, T., eds), János Bolyai Mathematical Society, pp. 355–397.Google Scholar
[14] Lovász, L. (2007) Combinatorial Problems and Exercises, second edition, AMS.Google Scholar
[15] Lovász, L. and Winkler, P. (1995) Efficient stopping rules for Markov chains. In Proc. 27th Annual ACM Symposium on Theory of Computing: STOC '95, ACM, pp. 76–82.CrossRefGoogle Scholar
[16] Lovász, L. and Winkler, P. (1995) Mixing of random walks and other diffusions on a graph. In Surveys in Combinatorics, 1995 (Rowlinson, P., ed.), Vol. 218 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 119–154.Google Scholar
[17] Lovász, L. and Winkler, P. (1998) Reversal of Markov chains and the forget time. Combin. Probab. Comput. 7 189–204.Google Scholar
[18] Pitman, J. W. (1977) Occupation measures for Markov chains. Adv. Appl. Probab. 9 69–86.CrossRefGoogle Scholar
[19] Winkler, P. (2014) Personal communication.Google Scholar
[20] Xu, H. and Yau, S.-T. (2013) Discrete Green's functions and random walks on graphs. J. Combin. Theory Ser. A 120 483–499.Google Scholar