Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T14:46:57.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Finding independent transversals efficiently

Part of: Graph theory

Published online by Cambridge University Press:  14 May 2020

Alessandra Graf  and
Penny Haxell
Alessandra Graf*
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON, N2L 3G1, Canada
Penny Haxell
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON, N2L 3G1, Canada
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an efficient algorithm that, given a graph G and a partition V1,…,Vm of its vertex set, finds either an independent transversal (an independent set {v1,…,vm} in G such that 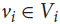${v_i} \in {V_i}$ for each i), or a subset 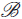${\cal B}$ of vertex classes such that the subgraph of G induced by 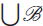$\bigcup\nolimits_{\cal B}$ has a small dominating set. A non-algorithmic proof of this result has been known for a number of years and has been used to solve many other problems. Thus we are able to give algorithmic versions of many of these applications, a few of which we describe explicitly here.

MSC classification

Primary: 05C69: Dominating sets, independent sets, cliques
Secondary: 05C85: Graph algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 5 , September 2020 , pp. 780 - 806
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achlioptas, D. and Iliopoulos, F. (2016) Random walks that find perfect objects and the Lovász Local Lemma. J. Assoc. Comput. Mach. 63 22.10.1145/2818352CrossRefGoogle Scholar
Aharoni, R. (2001) Ryser’s conjecture for tripartite 3-graphs. Combinatorica 21 1–4.CrossRefGoogle Scholar
Aharoni, R. and Berger, E. (2006) The intersection of a matroid and a simplicial complex. Trans. Amer. Math. Soc. 358 4895–4917.10.1090/S0002-9947-06-03833-5CrossRefGoogle Scholar
Aharoni, R., Berger, E. and Ziv, R. (2007) Independent systems of representatives in weighted graphs. Combinatorica 27 253–267.CrossRefGoogle Scholar
Aharoni, R., Chudnovsky, M. and Kotlov, A. (2002) Triangulated spheres and colored cliques. Discrete Comput. Geom. 28 223–229.CrossRefGoogle Scholar
Aharoni, R. and Haxell, P. (2000) Hall’s theorem for hypergraphs. J. Graph Theory 35 83–88.3.0.CO;2-V>CrossRefGoogle Scholar
Alon, N. (1988) The linear arboricity of graphs. Israel J. Math. 62 311–325.CrossRefGoogle Scholar
Alon, N. (1991) A parallel algorithmic version of the local lemma. In Thirty-Second Annual Symposium on Foundations of Computer Science, pp. 586–593, IEEE.Google Scholar
Alon, N. (1992) The strong chromatic number of a graph. Random Struct. Algorithms 3 1–7.CrossRefGoogle Scholar
Alon, N. (2003) Problems and results in extremal combinatorics I. Discrete Math. 273 31–53.CrossRefGoogle Scholar
Alon, N. and Asodi, V. (2007) Edge colouring with delays. Combin. Probab. Comput. 16 173–191.CrossRefGoogle Scholar
Alon, N., Ding, G., Oporowski, B. and Vertigan, D. (2003) Partitioning into graphs with only small components. J. Combin. Theory Ser. B 87 231–243.CrossRefGoogle Scholar
Alon, N. and Spencer, J. (2008) The Probabilistic Method, third edition, Wiley.CrossRefGoogle Scholar
Annamalai, C. (2016) Finding perfect matchings in bipartite hypergraphs. In Twenty-Seventh Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 1814–1823.CrossRefGoogle Scholar
Annamalai, C. (2017) Algorithmic advances in allocation and scheduling. PhD dissertation, ETH Zurich.Google Scholar
Annamalai, C. (2018) Finding perfect matchings in bipartite hypergraphs. Combinatorica 38 1285–1307.CrossRefGoogle Scholar
Asadpour, A., Feige, U. and Saberi, A. (2008) Santa Claus meets hypergraph matchings. In APPROX 2008 and RANDOM 2008 (Goel, A.et al., eds), Vol. 5171 of Lecture Notes in Computer Science, pp. 10–20, Springer.CrossRefGoogle Scholar
Asadpour, A., Feige, U. and Saberi, A. (2012) Santa Claus meets hypergraph matchings. ACM Trans. Algorithms 8 24.CrossRefGoogle Scholar
Beck, J. (1991) An algorithmic approach to the Lovász Local Lemma. Random Struct. Algorithms 2 343–365.CrossRefGoogle Scholar
Bissacot, R., Fernández, R., Procacci, A. and Scoppola, B. (2011) An improvement of the Lovász local lemma via cluster expansion. Combin. Probab. Comput. 20 709–719.CrossRefGoogle Scholar
Bollobás, B., Erdős, P. and Szemerédi, E. (1975) On complete subgraphs of r-chromatic graphs. Discrete Math. 13 97–107.CrossRefGoogle Scholar
Britnell, J., Evseev, A., Guralnick, R., Holmes, P. and Maróti, A. (2008) Sets of elements that pairwise generate a linear group. J. Combin. Theory Ser. A 115 442–465.CrossRefGoogle Scholar
Chandrasekaran, K., Goyal, N. and Haeupler, B. (2013) Deterministic algorithms for the Lovász local lemma. SIAM J. Comput. 42 2132–2155.CrossRefGoogle Scholar
Christofides, D., Edwards, K. and King, A. (2013) A note on hitting maximum and maximal cliques with a stable set. J. Graph Theory 73 354–360.CrossRefGoogle Scholar
Czumaj, A. and Scheideler, C. (2000) Coloring non-uniform hypergraphs: a new algorithmic approach to the general Lovász local lemma. In Eleventh Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 30–39.Google Scholar
Erdős, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In Infinite and Finite Sets (Keszthely, Hungary 1973), Vol. 10 of Colloquia Mathematica Societatis János Bolyai, pp. 609–627.Google Scholar
Fellows, M. (1990) Transversals of vertex partitions in graphs. SIAM J. Discrete Math. 3 206–215.CrossRefGoogle Scholar
Fischer, M. and Ghaffari, M. (2017) Subalgorithmic distributed algorithms for Lovász local lemma and the complexity hierarchy. In Thirty-First International Symposium on Distributed Computing, Vol. 91 of Leibniz International Proceedings in Informatics (LIPIcs), pp. 18:1–18.16, Schloss Dagstuhl–Leibniz-Zentrum für Informatik.Google Scholar
Graf, A. (2019) Finding independent transversals efficiently. PhD dissertation, University of Waterloo.CrossRefGoogle Scholar
Graf, A., Harris, D. and Haxell, P. Algorithms for weighted independent transversals and strong colouring, submittedGoogle Scholar
Harris, D. (2016) Lopsidependency in the Moser–Tardos framework: beyond the lopsided local lemma. ACM Trans. Algorithms 13 17.CrossRefGoogle Scholar
Harris, D. (2018) Derandomizing the Lovász local lemma via log-space statistical tests. arXiv:1807.06672Google Scholar
Harris, D. and Srinivasan, A. (2013) The Moser–Tardos framework with partial resampling. In IEEE Fifty-Fourth Annual Symposium on Foundations of Computer Science, pp. 469–478.CrossRefGoogle Scholar
Harris, D. and Srinivasan, A. (2014) A constructive algorithm for the Lovász local lemma on permutations. In Twenty-Fifth Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 907–925.CrossRefGoogle Scholar
Harris, D. and Srinivasan, A. (2017) A constructive Lovász local lemma for permutations. Theory Comput. 13 1–41.CrossRefGoogle Scholar
Haxell, P. (1995) A condition for matchability in hypergraphs. Graphs Combin. 11 245–248.CrossRefGoogle Scholar
Haxell, P. (1995) A note on a conjecture of Ryser. Periodica Math. Hungar. 30 73–79.CrossRefGoogle Scholar
Haxell, P. (2001) A note on vertex list colouring. Combin. Probab. Comput. 10 345–347.CrossRefGoogle Scholar
Haxell, P. (2004) On the strong chromatic number. Combin. Probab. Comput. 13 857–865.CrossRefGoogle Scholar
Haxell, P. (2008) An improved bound for the strong chromatic number. J. Graph Theory 58 148–158.CrossRefGoogle Scholar
Haxell, P. (2011) On forming committees. Amer. Math. Monthly 118 777–788.CrossRefGoogle Scholar
Haxell, P. and Szabó, T. (2006) Odd independent transversals are odd. Combin. Probab. Comput. 15 193–211,.CrossRefGoogle Scholar
Haxell, P., Szabó, T. and Tardos, G. (2003) Bounded size components: partitions and transversals. J. Combin. Theory Ser. B 88 281–297.CrossRefGoogle Scholar
Jin, G. (1992) Complete subgraphs of r-partite graphs. Combin. Probab. Comput. 1 241–250.CrossRefGoogle Scholar
Kaiser, T., Král, D. and Škrekovski, R. (2004) A revival of the girth conjecture. J. Combin. Theory Ser. B 92 41–53.CrossRefGoogle Scholar
Kaiser, T., Král, D., Škrekovski, R. and Zhu, X. (2007) The circular chromatic index of graphs of high girth. J. Combin. Theory Ser. B 97 1–13.CrossRefGoogle Scholar
King, A. (2011) Hitting all maximum cliques with a stable set using lopsided independent transversals J. Graph Theory 67 300–305.CrossRefGoogle Scholar
Kolipaka, K. and Szegedy, M. (2011) Moser and Tardos meet Lovász. In Forty-Third Annual ACM Symposium on Theory of Computing, pp. 235–244.CrossRefGoogle Scholar
Kolipaka, K., Szegedy, M. and Xu, Y. (2012) A sharper local lemma with improved applications. In Approximation, Randomization, and Combinatorial Optimization, Vol. 7408 of Lecture Notes in Computer Science, pp. 603–614, Springer.Google Scholar
Krivelevich, M. (1997) Almost perfect matchings in random uniform hypergraphs. Discrete Math. 170 259–263.CrossRefGoogle Scholar
Meshulam, R. (2001) The clique complex and hypergraph matching. Combinatorica 21 89–94.CrossRefGoogle Scholar
Molloy, M. and Reed, B. (1998) Further algorithmic aspects of the local lemma. In Thirtieth Annual ACM Symposium on Theory of Computing, pp. 524–529.CrossRefGoogle Scholar
Moser, R. (2009) A constructive proof of the Lovász Local Lemma. In Forty-First Annual ACM Symposium on Theory of Computing, pp. 343–350.CrossRefGoogle Scholar
Moser, R. and Tardos, G. (2010) A constructive proof of the general Lovász Local Lemma. J. Assoc. Comput. Mach. 57 11.CrossRefGoogle Scholar
Pegden, W. (2014) An extension of the Moser–Tardos algorithmic local lemma, SIAM J. Discrete Math. 28 911–917.CrossRefGoogle Scholar
Rabern, L. (2011) On hitting all maximum cliques with an independent set. J. Graph Theory 66 32–37.CrossRefGoogle Scholar
Reed, B. (2001) Perfect Graphs, Wiley.Google Scholar
Srinivasan, A. (2008) Improved algorithmic versions of the Lovász local lemma. In Nineteenth Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 611–620.Google Scholar
Szabó, T. and Tardos, G. (2006) Extremal problems for transversals in graphs with bounded degree. Combinatorica 26 333–351.CrossRefGoogle Scholar
Yuster, R. (1997) Independent transversals in r-partite graphs. Discrete Math. 176 255–261.CrossRefGoogle Scholar