Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T04:10:57.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Edge-statistics on large graphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  14 November 2019

Noga Alon ,
Dan Hefetz ,
Michael Krivelevich  and
Mykhaylo Tyomkyn
Noga Alon
Affiliation:
Department of Mathematics, Princeton University, Princeton, New Jersey, USA School of Mathematics and Computer Science, Tel Aviv University, Tel Aviv, Israel
Dan Hefetz
Affiliation:
Department of Computer Science, Ariel University, Ariel40700, Israel
Michael Krivelevich
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv6997801, Israel
Mykhaylo Tyomkyn*
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv6997801, Israel Department of Mathematics, California Institute of Technology, Pasadena, CA91125
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The inducibility of a graph H measures the maximum number of induced copies of H a large graph G can have. Generalizing this notion, we study how many induced subgraphs of fixed order k and size ℓ a large graph G on n vertices can have. Clearly, this number is 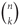$\left( {\matrix{n \cr k}}\right)$ for every n, k and 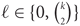$\ell \in \left\{ {0,\left( {\matrix{k \cr 2}} \right)}\right\}$. We conjecture that for every n, k and 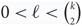$0 \lt \ell \lt \left( {\matrix{k \cr 2}}\right)$ this number is at most 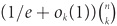$ (1/e + {o_k}(1)) {\left( {\matrix{n \cr k}} \right)}$. If true, this would be tight for ℓ ∈ {1, k − 1}.

In support of our ‘Edge-statistics Conjecture’, we prove that the corresponding density is bounded away from 1 by an absolute constant. Furthermore, for various ranges of the values of ℓ we establish stronger bounds. In particular, we prove that for ‘almost all’ pairs (k, ℓ) only a polynomially small fraction of the k-subsets of V(G) have exactly ℓ edges, and prove an upper bound of 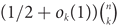$ (1/2 + {o_k}(1)){\left( {\matrix{n \cr k}}\right)}$ for ℓ = 1.

Our proof methods involve probabilistic tools, such as anti-concentration results relying on fourth moment estimates and Brun’s sieve, as well as graph-theoretic and combinatorial arguments such as Zykov’s symmetrization, Sperner’s theorem and various counting techniques.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 2 , March 2020 , pp. 163 - 189
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by NSF grant DMS-1855464, ISF grant 281/17, BSF grant 2018267 and the Simons Foundation.

‡

The research of Dan Hefetz is supported by ISF grant 822/18.

§

Partially supported by USA-Israel BSF grants 2014361 and 2018267, and by ISF grant 1261/17.

The research of Mykhaylo Tyomkyn is supported in part by ERC Starting Grant 633509.

References

Ahlswede, R. and Katona, G. O. H. (1978) Graphs with maximal number of adjacent pairs of edges. Acta Math. Acad. Sci. Hungar. 32 97–120.CrossRefGoogle Scholar
Alon, N., Gutin, G. and Krivelevich, M. (2004) Algorithms with large domination ratio. J. Algorithms 50 118–131.CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The Probabilistic Method, fourth edition, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.Google Scholar
Balogh, J., Hu, P., Lidický, B. and Pfender, F. (2016) Maximum density of induced 5-cycle is achieved by an iterated blow-up of 5-cycle. Eur. J. Combin. 52 47–58.CrossRefGoogle Scholar
Bollobás, B. (1998) Modern Graph Theory, Springer.CrossRefGoogle Scholar
Brown, J. I. and Sidorenko, A. (1994) The inducibility of complete bipartite graphs. J. Graph Theory 18 629–645.CrossRefGoogle Scholar
Erdős, P. (1945) On a lemma of Littlewood and Offord. Bull. Amer. Math. Soc. 51 898–902.CrossRefGoogle Scholar
Feige, U. (2004) On sums of independent random variables with unbounded variance, and estimating the average degree in a graph. In Proceedings of the Thirty-Sixth Annual ACM Symposium on the Theory of Computing, ACM, pp. 594–603.CrossRefGoogle Scholar
Fox, J. and Sauermann, L. (2018) A completion of the proof of the Edge-statistics Conjecture. arXiv:1809.01352Google Scholar
Hefetz, D. and Tyomkyn, M. (2018) On the inducibility of cycles. J. Combin. Theory Ser. B 133 243–258.CrossRefGoogle Scholar
Král, D., Norin, S. and Volec, J. (2018) A bound on the inducibility of cycles. arXiv:1801.01556Google Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.CrossRefGoogle Scholar
Kahn, J., Saks, M. and Smyth, C. (2011) The dual BKR inequality and Rudich’s conjecture. Combin. Probab. Comput 20 257–266.CrossRefGoogle Scholar
Kwan, M., Sudakov, B. and Tran, T. (2019) Anticoncentration for subgraph statistics. J. Lond. Math. Soc. 99 757–777.CrossRefGoogle Scholar
Martinsson, A., Mousset, F., Noever, A. and Trujić, M. (2018) The edge-statistics conjecture for ℓ ≪ k 6/5. arXiv:1809.02576Google Scholar
Pippenger, N. and Golumbic, M. C. (1975) Inducibility of graphs. J. Combin. Theory Ser. B 19 189–203.CrossRefGoogle Scholar
Yuster, R. (2018) On the exact maximum induced density of almost all graphs and their inducibility. arXiv:1801.01047Google Scholar
Zykov, A. A. (1949) On some properties of linear complexes. Mat. Sbornik N.S. 24 163–188.Google Scholar