Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T13:38:20.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Disjointness graphs of segments in the space

Part of: Graph theory

Published online by Cambridge University Press:  04 November 2020

János Pach ,
Gábor Tardos  and
Géza Tóth
János Pach*
Affiliation:
Rényi Institute, Budapest, Hungary Moscow Institute of Physics and Technology, Dolgoprudny, Russian Federation
Gábor Tardos
Affiliation:
Rényi Institute, Budapest, Hungary Moscow Institute of Physics and Technology, Dolgoprudny, Russian Federation
Géza Tóth
Affiliation:
Rényi Institute, Budapest, Hungary
*
*Corresponding author. Email: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The disjointness graph G = G(𝒮) of a set of segments 𝒮 in 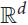${\mathbb{R}^d}$, 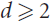$$d \ge 2$$, is a graph whose vertex set is 𝒮 and two vertices are connected by an edge if and only if the corresponding segments are disjoint. We prove that the chromatic number of G satisfies 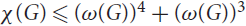$\chi (G) \le {(\omega (G))^4} + {(\omega (G))^3}$, where ω(G) denotes the clique number of G. It follows that 𝒮 has Ω(n1/5) pairwise intersecting or pairwise disjoint elements. Stronger bounds are established for lines in space, instead of segments.

We show that computing ω(G) and χ(G) for disjointness graphs of lines in space are NP-hard tasks. However, we can design efficient algorithms to compute proper colourings of G in which the number of colours satisfies the above upper bounds. One cannot expect similar results for sets of continuous arcs, instead of segments, even in the plane. We construct families of arcs whose disjointness graphs are triangle-free (ω(G) = 2), but whose chromatic numbers are arbitrarily large.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C62: Graph representations (geometric and intersection representations, etc.) 05C85: Graph algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 4 , July 2021 , pp. 498 - 512
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by the National Research, Development and Innovation Office (NKFIH) project KKP-133864, ERC Advanced Grant ‘GeoScape’, the Austrian Science Fund grant Z 342-N31, and by the Ministry of Education and Science of the Russian Federation in the framework of MegaGrant no. 075-15-2019-1926.

‡

Supported by the Cryptography ‘Lendület’ project of the Hungarian Academy of Sciences and by the National Research, Development and Innovation Office (NKFIH) projects K-116769, K-132696 and KKP-133864, by the ERC Synergy Grant ‘Dynasnet’ no. 810115 and by the Ministry of Education and Science of the Russian Federation in the framework of MegaGrant no. 075-15-2019-1926.

§

Supported by National Research, Development and Innovation Office, NKFIH, K-131529, KKP-133864, NKFIH-1158-6/2019 and by the Higher Educational Institutional Excellence Program 2019.

References

Alimonti, P. and Kann, V. (2000) Some APX-completeness results for cubic graphs. Theoret. Comput. Sci. 237 123–134.CrossRefGoogle Scholar
Asplund, E. and Grünbaum, B. (1960) On a colouring problem. Math. Scand. 8 181–188.CrossRefGoogle Scholar
Berge, C. (1961) Färbung von Graphen, deren sämtliche bzw. deren ungerade Kreise starr sind. Beiträge zur Graphentheorie (Vorträge während des graphentheoretischen Kolloquiums in Halle im März 1960, German). Wiss. Zeitschr. Univ. Halle 10 114.Google Scholar
Bollobás, B. (1998) Modern Graph Theory, Vol. 184 of Graduate Texts in Mathematics. Springer.CrossRefGoogle Scholar
Burling, J. P. (1965) On coloring problems of families of prototypes. PhD thesis, University of Colorado, Boulder.Google Scholar
Cabello, S., Cardinal, J. and Langerman, S. (2013) The clique problem in ray intersection graphs. Discrete Comput. Geom. 50 771–783.CrossRefGoogle Scholar
Cardinal, J., Payne, M. S. and Solomon, N. (2016) Ramsey-type theorems for lines in 3-space. Discrete Math. Theoret. Comput. Sci. 18 14.Google Scholar
Chalermsook, P. and Walczak, B. (2019) Personal communication, Prague, September 2019.Google Scholar
Davies, J. and McCarty, R. (2019) Circle graphs are quadratically χ-bounded. arXiv:1905.11578.Google Scholar
Dilworth, R. P. (1950) A decomposition theorem for partially ordered sets. Ann. of Math. 51 161–166.CrossRefGoogle Scholar
Dirac, G. A. (1961) On rigid circuit graphs. Abh. Math. Sem. Univ. Hamburg 25 71–76.CrossRefGoogle Scholar
Ehrlich, G., Even, S. and Tarjan, R. E. (1976) Intersection graphs of curves in the plane. J. Combin. Theory Ser. B 21 8–20.CrossRefGoogle Scholar
Erdős, P. and Hajnal, A. (1964) Some remarks on set theory, IX: Combinatorial problems in measure theory and set theory. Michigan Math. J. 11 107–127.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y. (1991) A density version of the Hales–Jewett theorem, J. Anal. Math. 57 64–119.CrossRefGoogle Scholar
Gavril, F. (1974) The intersection graphs of subtrees in trees are exactly the chordal graphs. J. Combin. Theory Ser. B 16 47–56.CrossRefGoogle Scholar
Grötschel, M., Lovász, L. and Schrijver, A. (1988) Geometric Algorithms and Combinatorial Optimization. Springer.CrossRefGoogle Scholar
Gyárfás, A. (1985) On the chromatic number of multiple interval graphs and overlap graphs. Discrete Math. 55 161–166. Corrigendum: Discrete Math. 62 (1986) 333.CrossRefGoogle Scholar
Gyárfás, A. (1987) Problems from the world surrounding perfect graphs. Applicationes Mathematicae 19 413–441.CrossRefGoogle Scholar
Gyárfás, A. and Lehel, J. (1983) Hypergraph families with bounded edge cover or transversal number. Combinatorica 3 351–358.CrossRefGoogle Scholar
Gyárfás, A. and Lehel, J. (1985) Covering and coloring problems for relatives of intervals. Discrete Math. 55 167–180.CrossRefGoogle Scholar
Hajnal, A. and Surányi, J. (1958) Über die Auflösung von Graphen in vollständige Teilgraphen (German). Ann. Univ. Sci. Budapest. Eötvös. Sect. Math. 1 113–121.Google Scholar
Hajós, G. (1957) Über eine Art von Graphen. Intern. Math. Nachr. 11 65.Google Scholar
Hilbert, D. and Cohn-Vossen, S. (1952) Geometry and the Imagination. Chelsea.Google Scholar
Holyer, I. (1981) The NP-completeness of edge-coloring. SIAM J. Comput. 10 718–720.CrossRefGoogle Scholar
Károlyi, G. (1991) On point covers of parallel rectangles. Period. Math. Hungar. 23 105–107.CrossRefGoogle Scholar
Károlyi, G., Pach, J. and Tóth, G. (1997) Ramsey-type results for geometric graphs, I. In ACM Symposium on Computational Geometry (Philadelphia, PA, 1996) . Discrete Comput. Geom. 18 247–255.CrossRefGoogle Scholar
Kostochka, A. V. (1988) Upper bounds for the chromatic numbers of graphs. Trudy Inst. Mat. (Novosibirsk), Modeli i Metody Optim. (Russian) 10 204–226.Google Scholar
Kostochka, A. V. (2004) Coloring intersection graphs of geometric figures. In Towards a Theory of Geometric Graphs (Pach, J., ed.), Vol. 342 of Contemporary Mathematics, pp. 127–138. American Mathematical Society.Google Scholar
Kostochka, A. V. and Kratochvíl, J. (1997) Covering and coloring polygon-circle graphs. Discrete Math. 163 299–305.CrossRefGoogle Scholar
Kratochvíl, J. and Nešetřil, J. (1990) INDEPENDENT SET and CLIQUE problems in intersection-defined classes of graphs. Comment. Math. Univ. Carolin. 31 85–93.Google Scholar
Kynčl, J. (2012) Ramsey-type constructions for arrangements of segments. European J. Combin. 33 336–339.CrossRefGoogle Scholar
Larman, D., Matoušek, J., Pach, J. and Töröcsik, J. (1994) A Ramsey-type result for convex sets. Bull. London Math. Soc. 26 132–136.CrossRefGoogle Scholar
Lovász, L. (1972) Normal hypergraphs and the perfect graph conjecture. Discrete Math. 2 253–267.CrossRefGoogle Scholar
Lovász, L. (1978) Kneser’s conjecture, chromatic number, and homotopy. J. Combin. Theory Ser. A 25 319–324.CrossRefGoogle Scholar
Lovász, L. (1993) Combinatorial Problems and Exercises, second edition. North-Holland.Google Scholar
Mütze, T., Walczak, B. and Wiechert, V. (2018) Realization of shift graphs as disjointness graphs of 1-intersecting curves in the plane. arXiv:1802.09969Google Scholar
Norin, S. (2017) Problem session at the Geometric and Structural Graph Theory workshop, Banff, August 20–25, 2017.Google Scholar
Pach, J. and Tomon, I. (2019) On the chromatic number of disjointness graphs of curves. In 35th International Symposium on Computational Geometry (SoCG 2019), pp. 54.1–54.17. Schloss Dagstuhl–Leibniz-Zentrum für Informatik.Google Scholar
Pawlik, A., Kozik, J., Krawczyk, T., Lasoń, M., Micek, P., Trotter, W. T. and Walczak, B. (2014) Triangle-free intersection graphs of line segments with large chromatic number. J. Combin. Theory Ser. B 105 6–10.CrossRefGoogle Scholar
Poljak, S. (1974) A note on stable sets and colorings of graphs. Comment. Math. Univ. Carolin. 15 307–309.Google Scholar