Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T08:21:42.257Z Has data issue: false hasContentIssue false
  • English
  • Français

A Convexity Property of Discrete Random Walks

Part of: Markov processes Stochastic processes Geometric function theory

Published online by Cambridge University Press:  31 March 2016

GÁBOR V. NAGY  and
VILMOS TOTIK
GÁBOR V. NAGY
Affiliation:
Bolyai Institute, University of Szeged, Szeged, Aradi v. tere 1, 6720, Hungary (e-mail: [email protected])
VILMOS TOTIK
Affiliation:
MTA-SZTE Analysis and Stochastics Research Group, Bolyai Institute, University of Szeged, Szeged, Aradi v. tere 1, 6720, Hungary and Department of Mathematics and Statistics, University of South Florida, 4202 E. Fowler Ave, CMC342, Tampa, FL 33620-5700, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish a convexity property for the hitting probabilities of discrete random walks in 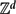${\mathbb Z}^d$ (discrete harmonic measures). For d = 2 this implies a recent result on the convexity of the density of certain harmonic measures.

MSC classification

Primary: 60J45: Probabilistic potential theory
Secondary: 60G50: Sums of independent random variables; random walks 30C85: Capacity and harmonic measure in the complex plane
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 6 , November 2016 , pp. 928 - 940
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Armitage, D. H. and Gardiner, S. J. (2002) Classical Potential Theory, Springer.Google Scholar
[2] Benko, D., Dragnev, P. and Totik, V. (2012) Convexity of harmonic densities. Rev. Mat. Iberoam. 28 1–14.Google Scholar
[3] Billingsley, P. (1968) Convergence of Probability Measures, Wiley.Google Scholar
[4] Courant, R., Friedrichs, K. and Lewy, H. (1928) Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 100 32–74.Google Scholar
[5] Doob, J. L. (1984) Classical Potential Theory and its Probabilistic Counterpart, Springer.Google Scholar
[6] Garnett, J. B. and Marshall, D. E. (2005) Harmonic Measure, New Mathematical Monographs, Cambridge University Press.Google Scholar
[7] Guy, R. K., Krattenthaler, C. and Sagan, B. E. (1992) Lattice paths, reflections, and dimension-changing bijections. Ars Combin. 34 3–15.Google Scholar
[8] Kallenberg, O. (1997) Foundations of Modern Probability, Probability and Its Applications, Springer.Google Scholar
[9] Port, S. C. and Stone, C. J. (1978) Brownian Motion and Classical Potential Theory, Probability and Mathematical Statistics, Academic.Google Scholar
[10] Ransford, T. (1995) Potential Theory in the Complex Plane, Cambridge University Press.Google Scholar