Published online by Cambridge University Press: 12 September 2013
For k-graphs F0 and H, an F0-packing of H is a family 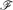 $\mathscr{F}$ of pairwise edge-disjoint copies of F0 in H. Let νF0(H) denote the maximum size |
$\mathscr{F}$ of pairwise edge-disjoint copies of F0 in H. Let νF0(H) denote the maximum size |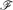 $\mathscr{F}$| of an F0-packing of H. Already in the case of graphs, computing νF0(H) is NP-hard for most fixed F0 (Dor and Tarsi [6]).
$\mathscr{F}$| of an F0-packing of H. Already in the case of graphs, computing νF0(H) is NP-hard for most fixed F0 (Dor and Tarsi [6]).
In this paper, we consider the case when F0 is a fixed linear k-graph. We establish an algorithm which, for ζ > 0 and a given k-graph H, constructs in time polynomial in |V(H)| an F0-packing of H of size at least νF0(H) − ζ |V(H)|k. Our result extends one of Haxell and Rödl, who established the analogous algorithm for graphs.