No CrossRef data available.
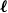 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence numberPublished online by Cambridge University Press: 24 April 2023
Given a graph
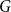 $G$
and an integer
$G$
and an integer
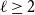 $\ell \ge 2$
, we denote by
$\ell \ge 2$
, we denote by
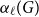 $\alpha _{\ell }(G)$
the maximum size of a
$\alpha _{\ell }(G)$
the maximum size of a
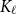 $K_{\ell }$
-free subset of vertices in
$K_{\ell }$
-free subset of vertices in
 $V(G)$
. A recent question of Nenadov and Pehova asks for determining the best possible minimum degree conditions forcing clique-factors in
$V(G)$
. A recent question of Nenadov and Pehova asks for determining the best possible minimum degree conditions forcing clique-factors in
 $n$
-vertex graphs
$n$
-vertex graphs
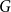 $G$
with
$G$
with
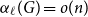 $\alpha _{\ell }(G) = o(n)$
, which can be seen as a Ramsey–Turán variant of the celebrated Hajnal–Szemerédi theorem. In this paper we find the asymptotical sharp minimum degree threshold for
$\alpha _{\ell }(G) = o(n)$
, which can be seen as a Ramsey–Turán variant of the celebrated Hajnal–Szemerédi theorem. In this paper we find the asymptotical sharp minimum degree threshold for
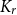 $K_r$
-factors in
$K_r$
-factors in
 $n$
-vertex graphs
$n$
-vertex graphs
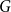 $G$
with
$G$
with
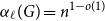 $\alpha _\ell (G)=n^{1-o(1)}$
for all
$\alpha _\ell (G)=n^{1-o(1)}$
for all
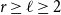 $r\ge \ell \ge 2$
.
$r\ge \ell \ge 2$
.