Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T00:46:47.493Z Has data issue: false hasContentIssue false
  • English
  • Français

An asymptotic bound for the strong chromatic number

Part of: Graph theory

Published online by Cambridge University Press:  15 March 2019

Allan Lo  and
Nicolás Sanhueza-Matamala
Allan Lo
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK
Nicolás Sanhueza-Matamala*
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The strong chromatic number χs(G) of a graph G on n vertices is the least number r with the following property: after adding 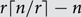$r\lceil n/r\rceil-n$ isolated vertices to G and taking the union with any collection of spanning disjoint copies of Kr in the same vertex set, the resulting graph has a proper vertex colouring with r colours. We show that for every c > 0 and every graph G on n vertices with Δ(G) ≥ cn, χs(G) ≤ (2+o(1))Δ(G), which is asymptotically best possible.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C70: Factorization, matching, partitioning, covering and packing 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 5 , September 2019 , pp. 768 - 776
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The research leading to these results was partially supported by EPSRC, grant no. EP/P002420/1.

‡

The research leading to these results was partially supported by the Becas Chile scholarship scheme from CONICYT.

References

Aharoni, R., Berger, E. and Ziv, R. (2007) Independent systems of representatives in weighted graphs. Combinatorica 27 253–267.CrossRefGoogle Scholar
Alon, N. (1988) The linear arboricity of graphs. Israel J. Math. 62 311–325.CrossRefGoogle Scholar
Alon, N. (1992) The strong chromatic number of a graph. Random Struct. Alg. 3 1–7.CrossRefGoogle Scholar
Axenovich, M. and Martin, R. (2006) On the strong chromatic number of graphs. SIAM J. Discrete Math. 20 741–747.CrossRefGoogle Scholar
Fellows, M. R. (1990) Transversals of vertex partitions in graphs. SIAM J. Discrete Math. 3 206–215.CrossRefGoogle Scholar
Fleischner, H. and Stiebitz, M. (1992) A solution to a colouring problem of P. Erdös. Discrete Math. 101 39–48.CrossRefGoogle Scholar
Fleischner, H. and Stiebitz, M. (1997) Some remarks on the cycle plus triangles problem. In The Mathematics of Paul Erdös II (R. Graham, L., and Nešetřil, J., eds), Vol. 14 of Algorithms and Combinatorics, Springer, pp. 136–142.CrossRefGoogle Scholar
Haxell, P. (1995) A condition for matchability in hypergraphs. Graphs Combin. 11 245–248.CrossRefGoogle Scholar
Haxell, P. (2001) A note on vertex list colouring. Combin. Probab. Comput. 10 345–347.CrossRefGoogle Scholar
Haxell, P. (2004) On the strong chromatic number. Combin. Probab. Comput. 13 857–865.CrossRefGoogle Scholar
Haxell, P. (2008) An improved bound for the strong chromatic number. J. Graph Theory 58 148–158.CrossRefGoogle Scholar
Haxell, P. (2016) Independent transversals and hypergraph matchings: An elementary approach. In Recent Trends in Combinatorics (Beveridge, A. et al., ed.), Vol. 159 of IMA Volumes in Mathematics and its Applications, Springer, pp. 215–233.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience.CrossRefGoogle Scholar
Johansson, A., Johansson, R. and Markström, K. (2010) Factors of r-partite graphs and bounds for the strong chromatic number. Ars Combin. 95 277–287.Google Scholar
Kahn, J. and Kayll, P. M. (1997) Fractional v. integral covers in hypergraphs of bounded edge size. J. Combin. Theory Ser. A 78 199–235.CrossRefGoogle Scholar
Krivelevich, M. (1997) Triangle factors in random graphs. Combin. Probab. Comput. 6 337–347.CrossRefGoogle Scholar
Lo, A. and Markström, K. (2013) A multipartite version of the Hajnal–Szemerédi theorem for graphs and hypergraphs. Combin. Probab. Comput. 22 97–111.CrossRefGoogle Scholar
Mubayi, D. and Zhao, Y. (2007) Co-degree density of hypergraphs. J. Combin. Theory Ser. A 114 1118–1132.CrossRefGoogle Scholar
Pippenger, N. Unpublished.Google Scholar
Rödl, V. e., Ruciński, A. and Szemerédi, E. (2006) A Dirac-type theorem for 3-uniform hypergraphs Combin. Probab. Comput. 15 229–251.CrossRefGoogle Scholar
Sachs, H. (1993) Elementary proof of the cycle-plus-triangles theorem. In Combinatorics: Paul Erdös is Eighty, Vol. 1, János Bolyai Mathematical Society, pp. 347–359.Google Scholar