Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dubickas, Artūras
2008.
An estimate for the probability of dependent events.
Statistics & Probability Letters,
Vol. 78,
Issue. 17,
p.
2839.
Dubickas, Artūras
2010.
On the distribution of powers of a complex number.
Archiv der Mathematik,
Vol. 95,
Issue. 2,
p.
151.
Dubickas, Artūras
2010.
Powers of Rational Numbers Modulo 1 Lying in Short Intervals.
Results in Mathematics,
Vol. 57,
Issue. 1-2,
p.
23.
Мощевитин, Николай Германович
and
Moshchevitin, Nikolai Germanovich
2010.
Сингулярные диофантовы системы А. Я. Хинчина и их применение.
Успехи математических наук,
Vol. 65,
Issue. 3,
p.
43.
Dubickas, Arturas
2011.
The lonely runner problem for many runners.
Glasnik matematicki,
Vol. 46,
Issue. 1,
p.
25.


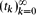 be a sequence of real numbers satisfying
be a sequence of real numbers satisfying 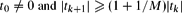 for each
for each 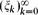 , there is a real number ξ such that
, there is a real number ξ such that 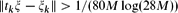 for each
for each 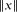 denotes the distance from
denotes the distance from 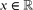 to the nearest integer. This is a corollary derived from our main theorem, which is a more general matrix version of this statement with explicit constants.
to the nearest integer. This is a corollary derived from our main theorem, which is a more general matrix version of this statement with explicit constants.