Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T03:02:04.416Z Has data issue: false hasContentIssue false
  • English
  • Français

A Solid-Solution Model for Fe(II)-Fe(III)-Mg(II) Green Rusts and Fougerite and Estimation of their Gibbs Free Energies of Formation

Published online by Cambridge University Press:  01 January 2024

Guilhem Boorrié ,
Fabienne Trolard ,
Philippe Refait  and
Frédéric Feder
Guilhem Boorrié*
Affiliation:
INRA, Unité de Recherche de Géochimie des Sols et des Eaux, URGSE, Europôle de l’Arbois, BP 80, F13545 Aix-en-Provence cedex 04, France
Fabienne Trolard
Affiliation:
INRA, Unité de Recherche de Géochimie des Sols et des Eaux, URGSE, Europôle de l’Arbois, BP 80, F13545 Aix-en-Provence cedex 04, France
Philippe Refait
Affiliation:
LEMMA, Université de La Rochelle, Bâtiment Marie Curie, 25 rue Enrico Fermi, F17000 La Rochelle, France
Frédéric Feder
Affiliation:
INRA, Unité de Recherche de Géochimie des Sols et des Eaux, URGSE, Europôle de l’Arbois, BP 80, F13545 Aix-en-Provence cedex 04, France CIRAD, Equipe “REGARD”, Station de La Bretagne, BP 20, F97408 Saint-Denis Messag, cedex 9, La Réunion, France
*
*E-mail address of corresponding author: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Fe(II)–Fe(III) green rust identified in soil as a natural mineral is responsible for the blue-green color of gley horizons, and exerts the main control on Fe dynamics. A previous EXAFS study of the structure of the mineral confirmed that the mineral belongs to the group of green rusts (GR), but showed that there is a partial substitution of Fe(II) by Mg(II), which leads to the general formula of the mineral: [Fe1−x2+Fex3+Mgy(OH)2+2y]x+[xOH−⋅mH2O]x−${[{\rm{Fe}}_{1 - x}^{2 + }{\rm{Fe}}_x^{3 + }{\rm{M}}{{\rm{g}}_y}{({\rm{OH}})_{2 + 2y}}]^{x + }}{[x{\rm{O}}{{\rm{H}}^ - } \cdot m{{\rm{H}}_2}{\rm{O}}]^{x - }}$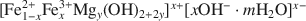. The regular binary solid-solution model proposed previously must be extended to ternary, with provision for incorporation of Mg in the mineral. Assuming ideal substitution between Mg(II) and Fe(II), the chemical potential of any Fe(II)-Fe(III)-Mg(II) hydroxy-hydroxide is obtained as: μ=X1μ1o+X2μ2o+X3μ3o+RT[X1lnX1+X2lnX2+X3lnX3]+A12X2(1−X2)${\rm{\mu }} = {X_1}{\rm{\mu }}_{\rm{1}}^{\rm{o}} + {X_2}{\rm{\mu }}_{\rm{2}}^{\rm{o}} + {X_3}{\rm{\mu }}_{\rm{3}}^{\rm{o}} + {\rm{R}}T[{X_1}{\rm{ln}}{X_1} + {X_2}{\rm{ln}}{X_2} + {X_3}{\rm{ln}}{X_3}] + {A_{12}}{X_2}(1 - {X_2})$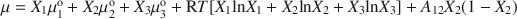. All experimental data show that the mole ratio X2 = Fe(III)/[Fetotal + Mg] is constrained (1) structurally and (2) geochemically. Structurally, Fe(III) ions cannot neighbor each other, which leads to the inequality X2α13.${X_2}\leqslant {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 3$}}.$ 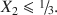Geochemically, Fe(III) cannot be too remote from each other for GR to form as Fe(OH)2 and Mg(OH)2 are very soluble, so X2α14${X_2}\geqslant {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 4$}}$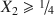. A linear relationship is obtained between the Gibbs free energy of formation of GR, normalized to one Fe atom, and the electronegativity ϰ of the interlayer anion, as: μo/n = −76.887ϰ — 491.5206 (r2 = 0.9985, N = 4), from which the chemical potential of the mineral fougerite μ is obtained in the limiting case X3 = 0, and knowing μ1o=−489.8${\rm{\mu }}_{\rm{1}}^{\rm{o}} = - 489.8$ 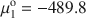kJmol−1 for Fe(OH)2, and μ3o=−832.16${\rm{\mu }}_{\rm{3}}^{\rm{o}} = - 832.16$ 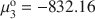kJmol−1 for Mg(OH)2, the two unknown thermodynamic parameters of the solid-solution model are determined as

μ2o=+119.18kJmol−1${\rm{\mu }}_{\rm{2}}^{\rm{o}} = + 119.18\;{\rm{kJmo}}{{\rm{l}}^{ - 1}}$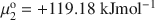 for Fe(OH)3 (virtual), and A12 = −1456.28 kJmol−1 (non-ideality parameter). From Mössbauer in situ measurements and our model, the chemical composition of the GR mineral is constrained into a narrow range and the soil solutions-mineral equilibria computed. Soil solutions appear to be largely overstaurated with respect to the two forms observed.

Keywords

FeFougeriteGleyGreen RustHydroxideMgModelOxideSoilThermodynamics
Type
Research Article
Information
Clays and Clay Minerals , Volume 52 , Issue 3 , June 2004 , pp. 382 - 394
Copyright
Copyright © 2004, The Clay Minerals Society

References

Abdelmoula, M. Trolard, F. Bourrié, G. and Génin, J-MR, (1998) Evidence for the Fe(II)–Fe(III) green rust Fougerite mineral occurrence in a hydromorphic soil and its transformation with depth Hyperfine Interactions 111 235–238 10.1023/A:1010802508927.CrossRefGoogle Scholar
Altmeier, M. Metz, V. Neck, V. Müller, R. and Fanghänel, T.h., (2003) Solid-liquid equilibria of Mg(OH)2 (cr) and Mg(OH)3 Cl-4H2O(cr) in the system Mg-Na-H-OH-Cl-H2O at 25°C Geochimica et Cosmochimica Acta 67 3595–3601 10.1016/S0016-7037(03)00165-0.Google Scholar
Arden, T.V. (1950) The solubility products of ferrous and ferrosic hydroxides. Journal of the Chemical Society, 882–885.Google Scholar
Bernal, J.D. Dasgupta, D.R. and Mackay, A.L., (1959) The oxides and hydroxides of iron and their structural interrelationships Clay Minerals Bulletin 14 882–885.Google Scholar
Bourrié, G., (1983) Rôle des composés amorphes dans le contrôle de la composition chimique des solutions du sol Science du Sol 3 195–204 4.Google Scholar
Bourrié, G. Trolard, F. Génin, J-MR Jaffrezic, A. Maître, V. and Abdelmoula, M., (1999) Iron control by equilibria between hydroxy-Green Rusts and solutions in hydromorphic soils Geochimica et Cosmochimica Acta 63 3417–3427 10.1016/S0016-7037(99)00262-8.Google Scholar
Bratsch, S.G., (1989) Standard electrode potentials and temperature coefficients in water at 298.15 K Journal of Physical and Chemical Reference Data 18 1–21 10.1063/1.555839.Google Scholar
Davies, P.K. and Navrotsky, A., (1983) Quantitative correlations of deviations from ideality in binary and pseudobinary solid solutions Journal of Solid State Chemistry 46 1–22 10.1016/0022-4596(83)90122-6.CrossRefGoogle Scholar
Détournay, J. De Miranda, L. Dérié, R. and Ghodsi, M., (1975) The region of stability of green rust II in the electrochemical E-pH equilibrium diagram of iron in sulphate medium Corrosion Science 15 295–306 10.1016/S0010-938X(75)80011-4.Google Scholar
Drissi, S.H. Refait, P.h. and Génin, J-MR, (1994) The oxidation of Fe(OH)2 in the presence of carbonate ions: structure of carbonate green rust one Hyperfine Interactions 90 395–400 10.1007/BF02069145.Google Scholar
Drissi, S.H. Refait, P.h. Abdelmoula, M. and Génin, J-MR, (1995) Preparation and thermodynamic properties of Fe(II)–Fe(III) hydroxide-carbonate (green rust one), Pourbaix diagram of iron in carbonate-containing aqueous media Corrosion Science 37 2025–2041 10.1016/0010-938X(95)00096-3.Google Scholar
Feder, F., (2001) Dynamique des processus d’oxydo-réduction dans les sols hydromorphes — monitoring in situ de la solution du sol et des phases solides ferrifères France Université d’Aix-Marseille III, Aix-en-Provence 200 pp.Google Scholar
Génin, J-MR Olowe, A.A. Refait, P.h. and Simon, L., (1996) On the stoichiometry and Pourbaix diagram of Fe(II)–Fe(III) hydroxy-sulphate or sulphate containing green rust 2; an electrochemical and Mössbauer spectroscopy study Corrosion Science 38 1751–1762 10.1016/S0010-938X(96)00072-8.Google Scholar
Génin, J-MR Simon, L. Refait, P.h. and Ortalli, I., (1996) Existence of sulphite-containing green rust one Proceedings ICAME 95 Bologna, Italy SIF 51–54 editor.Google Scholar
Génin, J-MR Abdelmoula, M. Refait, P.h. and Simon, L., (1998) Comparison of the Green Rust Two lamellar double hydroxide class with the Green Rust One pyroaurite class: Fe(II)–Fe(III) sulphate and selenate hydroxides Hyperfine Interactions 3 313–316 10.1023/A:1012638724990.CrossRefGoogle Scholar
Génin, J-MR Bourrié, G. Trolard, F. Abdelmoula, M. Jaffrezic, A. Refait, P.h. Maître, V. Humbert, B. and Herbillon, A., (1998) Thermodynamic equilibria in aqueous suspensions of synthetic and natural Fe(II)–Fe(III) Green Rusts: occurrences of the mineral in hydromorphic soils Environmental Science and Technology 31 1058–1068 10.1021/es970547m.CrossRefGoogle Scholar
Génin, J-MR Refait, P.h. Bourrié, G. Abdelmoula, M. and Trolard, F., (2001) Structure and stability of the Fe(II)–Fe(III) green rust “fougerite” mineral and its potential for reducing pollutants in soil solutions Applied Geochemistry 16 559–570 10.1016/S0883-2927(00)00043-3.Google Scholar
Girard, A. and Chaudron, G., (1935) Sur la constitution de la rouille Comptes-Rendus de l’Academie des Sciences, Paris 100 127–129.Google Scholar
Hansen, H.C.B., (1989) Composition, stabilisation and light absorption of Fe(II)–Fe(III) hydroxycarbonate (green rust) Clay Minerals 14 663–669 10.1180/claymin.1989.024.4.08.Google Scholar
Hansen, H.C.B. and Taylor, R.M., (1991) Formation of synthetic analogues of double metal-hydroxy carbonate minerals under controlled pH conditions: II. The synthesis of desautelsite Clay Minerals 16 507–525 10.1180/claymin.1991.026.4.06.Google Scholar
Hashimoto, K. and Misawa, T., (1973) The solubility of γFeOOH in perchloric acid at 15°C Corrosion Science 13 229–231 10.1016/0010-938X(73)90016-4.Google Scholar
Jolivet, J.P., (1994) De la solution à l’oxyde — Condensation des cations en solution aqueuse — Chimie de surface des oxydes Paris InterEditions / CNRS Editions 387 pp.Google Scholar
Koritnig, S. and Susse, P., (1975) Meixnerit, Mg6Al2(OH)18.4H2O, ein neues Magnesium-Aluminium-Hydroxid-Mineral Tschermaks Mineralogische Petrologische Mitteilungen 11 79–87 10.1007/BF01081303.Google Scholar
Mascolo, G. and Marino, O., (1980) A new synthesis and characterization of magnesium-aluminium hydroxides Mineralogical Magazine 43 619–621 10.1180/minmag.1980.043.329.09.Google Scholar
Murad, E. and Taylor, R.M., (1984) The Mössbauer spectra of hydroxycarbonate green rusts Clay Minerals 19 77–83 10.1180/claymin.1984.019.1.08.Google Scholar
Olowe, A.A. and Génin, J-MR, (1991) The mechanism of oxidation of Fe(II) hydroxide in sulphated aqueous media: importance of the initial ratio of the reactants Corrosion Science 32 965–984 10.1016/0010-938X(91)90016-I.CrossRefGoogle Scholar
Ponnamperuma, F.N. Tianco, E.M. and Loy, T., (1967) Redox equilibria in flooded soils: I. The iron hydroxide system Soil Science 103 374–382 10.1097/00010694-196706000-00002.Google Scholar
Prigogine, I. and Defay, R., (1946) Thermodynamique chimique conformément aux méthodes de Gibbs et De Donder Paris Dunod tome I, 348 pp., tome II, 430 pp.Google Scholar
Refait, P.h. Abdelmoula, M. and Génin, J-MR, (1998) Mechanisms of formation and structure of green rust one in aqueous corrosion of iron in the presence of chloride ions Corrosion Science 40 1547–1560 10.1016/S0010-938X(98)00066-3.Google Scholar
Refait, P.h. Abdelmoula, M. Trolard, F. Génin, J-MR Ehrhardt, J.-J. and Bourrié, G., (2001) Mössbauer and XAS study of a green rust mineral; the partial substitution of Fe2+ by Mg2+ American Mineralogist 86 731–739 10.2138/am-2001-5-613.Google Scholar
Refait, P.h. Bon, C. Simon, L. Bourrié, G. Trolard, F. Bessière, J. and Génin, J-MR, (1999) Chemical composition and Gibbs standard free energy of formation of Fe(II)–Fe(III) hydroxysulphate green rust and Fe(II) hydroxide Clay Minerals 34 499–510 10.1180/000985599546280.Google Scholar
Refait, P.h. Charton, A. and Génin, J-MR, (1998) Identification, composition, thermodynamic and structural properties of a pyroaurite-like iron(II)-iron(III) hydroxyoxalate Green Rust European Journal of Solid State Inorganic Chemistry 35 655–666 10.1016/S0992-4361(99)80006-X.Google Scholar
Refait, P.h. and Génin, J-MR, (1993) The oxidation of Ni(II)–Fe(II) hydroxides in chloride-containing aqueous media Corrosion Science 34 2059–2070 10.1016/0010-938X(93)90060-T.Google Scholar
Refait, P.h. Simon, L. Louis, C. and Génin, J-MR, (2000) Reduction of SeO42− anions and anoxic formation of iron(II)–iron(III) hydroxy-selenate green rust Environmental Science and Technology 34 819–825 10.1021/es990376g.Google Scholar
Roussel, H. Briois, V. Elkaim, E. de Roy, A. and Besse, J.P., (2000) Cationic order and structure of [Zn-Cr-Cl] and [Cu-Cr-Cl] layered double hydroxides: a XRD and EXAFS study Journal of Physical Chemistry B25 5915–5953 10.1021/jp0000735.Google Scholar
Shannon, R.D., (1976) Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides Acta Crystallographica A32 751–767 10.1107/S0567739476001551.Google Scholar
Simon, L. François, M. Refait, P.h. Renaudin, G. Lelaurain, M. and Génin, J-MR, (2003) Structure of the Fe(II-III) layered double hydroxysulphate green rust two from Rietveld analysis Solid State Sciences 5 327–334 10.1016/S1293-2558(02)00019-5.Google Scholar
Simon, L. Refait, P.h. and Génin, J-MR, (1998) Transformation of Fe(II)–Fe(III) hydroxysulphite into hydroxysulphate Green Rusts Hyperfine Interactions 112 217–220 10.1023/A:1010845107110.Google Scholar
Stampfl, P.P., (1969) Ein basisches Eisen-II-III-Karbonat in Rost Corrosion Science 9 185–187 10.1016/S0010-938X(69)80029-6.Google Scholar
Taylor, R.M. and Van Olphen, H., (1981) Color in soils and sediments. A review International Clay Conference 1981 Amsterdam Elsevier 749–761.Google Scholar
Taylor, R.M. and MacKenzie, R.M., (1980) The influence of aluminum on iron oxides. VI. The formation of Fe(II)–Al(III) hydroxy-chlorides, -sulfates, and -carbonates as new members of the pyroaurite group and their significance in soils Clays and Clay Minerals 28 179–187 10.1346/CCMN.1980.0280303.Google Scholar
Trolard, F. Abdelmoula, M. Bourrié, G. Humbert, B. and Génin, J-MR, (1996) Mise en évidence d’un constituant de type “rouilles vertes” dans les sols hydromorphes — Proposition de l’ existence d’un nouveau minéral: la “fougérite” Comptes-Rendus de l’Académie des Sciences, Paris 323IIa 1015–1022.Google Scholar
Trolard, F. Génin, J-MR Abdelmoula, M. Bourrié, G. Humbert, B. and Herbillon, A., (1997) Identification of a green rust mineral in a reductomorphic soil by Mössbauer and Raman spectroscopies Geochimica et Cosmochimica Acta 61 1107–1111 10.1016/S0016-7037(96)00381-X.CrossRefGoogle Scholar
Vucelic, M. Jones, W. and Moggridge, G.D., (1997) Cation ordering in synthetic layered double hydroxides Clays and Clay Minerals 45 803–813 10.1346/CCMN.1997.0450604.Google Scholar
Vysotskii, G.N., (1905) Gley Pochvovedeniye 4 291–327 (original paper in Russian). (1999) Gley. An abridged version of Vysotskii (1905) on the 257th Anniversary of the Russian Academy of Sciences. Eurasian Soil Science, 32, 1063–1068.Google Scholar
Wagman, D.D., Evans, W.H., Parker, V.B., Schumm, R.H., Halow, L., Bailey, S.M., Churney, K.L. and Nuttall, R.L. (1982) The NBS Tables of chemical thermodynamic properties. Selected values for inorganic and C1 and C2 organic substances in SI units. Journal of Physical and Chemical Reference Data, Supplement n o2, 11.Google Scholar