The electrical conductivity of saturated kaolinite clay-water-electrolyte systems of different particle size distributions and of illite and montmorillonite clays were determined over the frequency range of 50–108 c/s. The conductivity increases as the frequency increases, and the experimental values show two distinct dispersions, one in the low frequency range and the other in the high frequency range. The frequency range over which the first dispersion occurs is experimentally shown to be dependent on particle size. The average particle size is uniquely related to the frequency at which half the dispersion occurs. The magnitude of conductivity variation, the high frequency conductivity and the streaming potential values are related to the microscopic permeability coefficient. This microscopic permeability coefficient, evaluated from a knowledge of the above electrical properties, is shown to be uniquely related to the Darcy permeability coefficient at various consolidation states of the kaolinite clays. Similar unique relationships have been observed in illitic clays.

La conductivité électrique de systèmes saturés de kaolinite-eau-électrolyte à répartition variable des particles ainsi que d’argile du type illite en montmorillonite a été déterminée pour la gamme de fréquences allant de 50–108 périodes/sec. La conductivité augmente à mesure que la fréquence devient plus élevée et les valeurs expérimentales montrent deux dispersions distinctes, l’une dans la gamme de basses fréquences et l’autre dans la gamme de fréquences élevées. Les expériences montrent que la gamme de fréquences dans laquelle a lieu la première dispersion dépend des dimensions de la particule. La taille moyenne de la particule est en relation directe avec la fréquence à laquelle la moitié de la dispersion a lieu. L’importance de la variation de conductivité, la conductivité à fréquence élevée et les valeurs du potentiel d’écoulement sont mises en relation avec le coefficient de perméabilité microscopique. Le coefficient de perméabilité microscopique, évalué sur la base d’une connaissance des propriété électriques établies ci-dessus, est en relation directe avec la coefficient de perméabilité Darcy pour des états différents de consolidation des argiles du type kaolinite. Des relations du même genre ont été observées dans le cas des argiles illitiques.

Das elektrische Leitvermögen gesättigter Kaolinitton-Wasser-Elektrolytsysteme mit verschiedenen Teilchengrössenverteilungen und von Illit- und Montmorillonittonen wurde über einen Frequenzbereich von 50-108 Hz bestimmt. Das Leitvermögen wächst mit zunehmender Frequenz und die Versuchswerte zeigen zwei deutliche Streuungen, eine im Bereich der Niederfrequenzen und die andere im Bereich der Hochfrequenzen. Es wird durch Versuche dargelegt, dass der Frequenzbereich in welchem die erste Streuung auftritt von der Teilchengrösse abhängt. Die Durchschnittsgrösse der Teilchen steht in eindeutiger Beziehung zu der Frequenz bei welcher die Hälfte der Streuung auftritt. Der Schwinkungsbereich des Leitvermogens, das Hochfrequenzleitvermögen und die Strömungspotentialwerte stehen in Beziehung zum mikroskopischen Permeabilitätskoeffizienten. Es wird gezeigt, dass dieser aus der Kenntnis der obigen elektrischen Kenngrössen bestimmte mikroskopische Permeabilitätskoeffizient in den verschiedenen Verdichtungszuständen der Kaolinittone auf eindeutige Weise mit dem Darcy Permeabilitätskoeffizient in Verbindung steht. Ahnliche eindeutige Beziehungen sind auch bei den illitischen Tonen beobachtet worden.

Удельная электропроводность систем насыщенная каолинитовая глина-вода-злектролит с распределением различных размеров частиц, а также иллитовых и монтморил-лонитовых глин, определялась в диапазоне частот 50—108 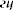. Электропроводность увеличивается по мере повышения частоты, а экспериментальные значения указывают две определенные дисперсии, одну в низкочастотном диапазоне, а вторуюбв-высокочастотном. Диапазон частот, в котором происходит первая дисперсия, зависит, как это доказано опытами, от размера частиц. Средний размер частиц уникально зависит от частоты, при которой происходит половина дисперсий. Величина изменений электропроводности, высокочастотная проводимость и потенциалы течения зависят от коэффициента микроскопической проница-емости. Этот коэффициент микроскопической проницаемости, вычисленный на основании вышеуказанных электрических свойств, показан уникально зависящим от коэффициента проницаемости Дарси в различных стадиях консолидации каолинитовых глин. Сходная зависимость наблюдается и в иллитовых глинах.