Published online by Cambridge University Press: 09 July 2018
Comme la plupart des vermiculites, l'hydrate à une couche de la vermiculite-Na (d001 = 11·85 Å) présente une structure semi-ordonnée, avec des défauts d'empilement (glissements selon l'axe b). Le plan (h0l)* du réseau réciproque est entièrement discret, tandis que les rangées n'appartenant pas à ce plan sont plus ou moins diffuses dans la direction c*. La projection x0z est obtenue par une classique analyse de Fourier bidimensionelle. Dans les plans (0kl)* et (1kl)*, certaines rangées semblent presque discrètes: ceci permet d'essayer de déterminer la translation 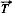 selon l'axe 0y entre deux feuillets adjacents. Le calcul des intensités des diffusions le long des rangées des plans (0kl)* et (1kl)* conduit à ne retenir qu'un seul modèle. Le désordre résulte d'une distribution aléatoire de trois translations parallèles à l'axe Oy: l'une est nulle et les deux autres sont de +0·307b et −0·307b. Le principal intérêt de ce travail est de présenter une nouvelle méthode d'approche pour l'étude des structures semi-ordonnées.
selon l'axe 0y entre deux feuillets adjacents. Le calcul des intensités des diffusions le long des rangées des plans (0kl)* et (1kl)* conduit à ne retenir qu'un seul modèle. Le désordre résulte d'une distribution aléatoire de trois translations parallèles à l'axe Oy: l'une est nulle et les deux autres sont de +0·307b et −0·307b. Le principal intérêt de ce travail est de présenter une nouvelle méthode d'approche pour l'étude des structures semi-ordonnées.
As in most vermiculites, the 11·85 Å Na-vermiculite phase has a semi-random structure with stacking faults along the b axis: the (h0l)* plane presents only discrete reflections while other reciprocal rows are more or less diffuse in the c* direction. The x0z projection is obtained by classical two-dimensional Fourier analysis. In the (0kl)* and (1kl)* planes, some rows appear almost discrete: this allows determination of the 0y translation 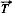 from one layer to the next. Calculation of the diffusion intensities along the rows of the (0kl)* and (1kl)* planes allows a single model to be derived. The disorder is created by the random distribution of three translations parallel to 0y: one is zero and the two others are +0·307b and −0·307b. This paper illustrates a new approach to the study of semi-random structures.
from one layer to the next. Calculation of the diffusion intensities along the rows of the (0kl)* and (1kl)* planes allows a single model to be derived. The disorder is created by the random distribution of three translations parallel to 0y: one is zero and the two others are +0·307b and −0·307b. This paper illustrates a new approach to the study of semi-random structures.