Article contents
Crystallochemical classifications of phyllosilicates based on the unified system of projection of chemical composition: I. The mica group
Published online by Cambridge University Press: 09 July 2018
Abstract
A unified system of vector representation of chemical composition is proposed for the phyllosilicates based on projection of the composition, as given by crystallochemical formula, onto a field with orthogonal axes chosen for octahedral divalent cations, R2+, and Si (X, Y, respectively), and oblique axes for octahedral trivalent cations, R3+, and vacancies, □, (V, Z, respectively). Point coordinates for each set of axes were used to define the direction and length of the unit vectors for phyllosilicates belonging to different groups. Parallel to these fundamental directions the composition isolines were drawn in the projection fields. Applied to micas, this system enables control of the chemical composition by the general crystallochemical formula covering all varieties of Li-free dioctahedral and trioctahedral micas:
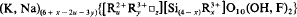
where z (number of vacancies) = (y-x+ m)/2; m (layer charge) =1; u+y+z = 3. There is a similar formula for vacancy-free lithian micas:
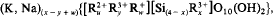
where w = m — x+y;m=1; u+y+w = 3, and for Li-free brittle micas:
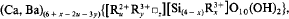
where z = (y — x+m)/2; m = 2; u+y+z = 3. Projection fields were used to classify micas.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Mineralogical Society of Great Britain and Ireland 1990
References
- 7
- Cited by


