^{page 105 note 1} This is not to be contradicted by Aristotle's statement (Met. A 992^a22; cf. M1084^b1–2) that Plato believed in indivisible lines. For there is more than one sort of mathematics according to Plato. Parm. 164 c–165 d, where magnitudes are infinitely divisible, applies to ‘popular' as opposed to ‘philosophical’ mathematics (v. Phil. 56 d–e; Rep. vii. 525d–526a). I hope to offer an explanation of this on another occasion.

^{page 105 note 2} Cf. Parm. 142 c 7–145 a 2.

^{page 105 note 3} Soph. 255 e, 256 e–257 a.

^{page 106 note 1} refers not merely to the diagram but to the fact that in Dialectic all Ideas start as hypotheses. For, incidentally, Plato never said there is an Idea corresponding to every general name, although this is now attributed to him by writer after writer. Rep. 59.6 a says 507 b . Cf. Phaedr. 237 d I for connexion with Socratic method.

^{page 106 note 2} For the use of ‘number’ where we should say ‘number of parts’–see Theaet. 204 d. But it has also an esoteric meaning, as is mentioned below.

^{page 107 note 1} Soph. 255 ff.

^{page 107 note 2} Ib. 256 e:

^{page 107 note 3} For the error of this view cf. 18 c 7–d 1. It is the same reason which has led to suspicion of the text—both and The latter was thought inconsistent with But to suppose too many species is similar to supposing too few: a wrongly supposed species (a instead of an Pol. 263) is no species at all and therefore has simply not taken place. Failure to emphasize this point makes Prof. Hackforth's note (C.Q. xxxiii (1939), 23–24)Google Scholar on this sentence a little unsatisfactory; especially so since his notes (Plato's Examination of Pleasure, 23–24) on our (4) and (5) do make the point.Google Scholar

^{page 108 note 1} Ar. Met. Z 1038^ag–25; De part. an. 642^b5–9.

^{page 108 note 2} (Procl. in I Eucl., ed. Friedlein, , p. 60. 15).Google Scholar

^{page 108 note 3} For this lesson in the Parmenides cf. 158^b2–d8; 164 c 7–d 8; 165 a 5–c 3.

^{page 108 note 4} Cf. Soph. 246 b 9–c 1: the Idealists repudiate the ‘reality’ of the materialists,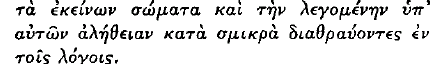

^{page 108 note 5} Ib. 258 d: (cf. 257 c 7). It is in respect of its having Being that Not-being is ‘chopped up’. The metaphor is, of course, explained by its being used for the division of a genus into species (Meno 79 a 1 o; c 2; Pol. 266 a 2).

^{page 108 note 6} As does Stenzel, , Studien z. Entw. d. plat. Dialektik² (Leipzig-Berlin 1931) 104,Google Scholar at least in Allan's interpretation ([Stenzel] Plato's method of Dialectic, tr. and ed. Allan, D. J., Oxford 1940, 146).Google Scholar Mr. Allan, who has very kindly read my manuscript, suggests that Stenzel ‘could say that , which has just been used in the dialectician's sense, (4), is then used as a man in the state of would use it, (5), i.e. “those alleged unities” ‘. But how many readers would grasp this from Plato's text?

^{page 109 note 1} Cf. Robin, L., Platon: Œuvres complètes, ii (1942), 184Google Scholar n. 20: ‘une fois qu'on est arrivé à l'espèce dernière … l'impossibilité de “specifier” davantage nous met en présence, et de l'individu, avec la multiplicité de ses caractères singuliers, et du nombre infini d'individus auxquels s'étend la notion de l'espèce derniere, avec tout ce qu'elle implique et qui constitue la chaîne des intermédiaires.’ But his translation ‘c'est alors que désormais on doit abandonner l'infini et lui dire adieu', is inexplicable.

^{page 109 note 2} Cf. Stenzel, J., Zahl u. Gestalt (1924), 7, 13–18;Google ScholarPreiswerk, A., ‘Das Einzelne b. Platon und Aristoteles’, Philologus, suppl.–Bd. xxxii, Heft 1 (1939), 55–56.Google Scholar

^{page 109 note 3} Cf. of (6) with the of 15 d–e, who ‘at one moment kneads any argument into one ball, then unrolls it again and chops it into pieces’. Compare also Phaedr. 237 d.

^{page 109 note 4} Nor elsewhere. (Pol. 286 e 6, despite Campbell's note, has nothing to do with the present point.)

^{page 110 note 1} Studien, 62–71 [tr. Allan, 96–10].Google Scholar

^{page 110 note 2} e.g. recently by Liebrucks, B., Platons Entw.z.Dialektik (Frankfurt-a.-M. 1949) 148.Google Scholar

^{page 110 note 3} The collection of parts is mentioned before the Division. Mr. Allan therefore suggests that, if a line is intended, a discontinuous one would be more comprehensible:

[For here some is required to see that stretches through from beginning to end.’

^{page 111 note 1} Cf. Parm. 145 b 8.

^{page 111 note 2} This is not to reject Ritter's, C. contention (Neue Untersuchungen über Platon (1910) 57Google Scholar ff.) that refers to the γ⋯νη like Otherness which is to the species of ordinary genera—though 250 b 8 is against it.

^{page 111 note 3} Plato's final interest, even in the Parm. passages, is not (pace Cornford, , Plato and Parmenides, 179 ff.)Google Scholar in infinite divisibility, but in a whole, i.e. genus, which is, and yet is more than, its parts. Cf. Theaet. 201 e–205 e with Ar. Met. Z 1041^b9–33 and the neglected passage, Hipp. ma. 300–2, which looks to me like a set piece of the Academy's Ideal theory.

^{page 111 note 4}

^{page 111 note 5} Budé edition, ad loc.

^{page 111 note 6} Pol. 262 b 6–7; 265 a 4. The reason is not that which a nominalist logic would give, viz. the exhaustiveness of a class-concept and its contradictory (although this doubtless influenced him in practice, especially in the Sophist), for a negative class is likely to be (cf. Pol. 262 d); cf. Ar. Met. A 990^b13 and Ross ad loc. (Platonists' denial ofldeas of negations).

^{page 112 note 1} Ar. Phys. Δ 213^b22; Met. N 1091^a17; fr. 201 (Rose).