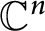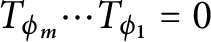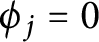Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Le, Trieu
Rodriguez, Tomas Miguel
and
Şahutoğlu, Sönmez
2025.
On Compactness of Products of Toeplitz Operators.
Complex Analysis and Operator Theory,
Vol. 19,
Issue. 1,