Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2025-01-03T18:04:13.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero and uniqueness sets for Fock spaces

Part of: Spaces and algebras of analytic functions Entire and meromorphic functions, and related topics Geometric function theory Linear function spaces and their duals

Published online by Cambridge University Press:  25 July 2022

D. Aadi  and
Y. Omari
D. Aadi
Affiliation:
Faculty of Sciences, CeReMAR, LAMA, Mohammed V University in Rabat, B.P. 1014 Rabat, Morocco e-mail: [email protected] [email protected]
Y. Omari*
Affiliation:
Faculty of Sciences, CeReMAR, LAMA, Mohammed V University in Rabat, B.P. 1014 Rabat, Morocco e-mail: [email protected] [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize zero sets for which every subset remains a zero set too in the Fock space 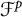$\mathcal {F}^p$ , 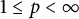$1\leq p<\infty $ . We are also interested in the study of a stability problem for some examples of uniqueness set with zero excess in Fock spaces.

Keywords

Fock spacesentire functionszero setsuniqueness sets

MSC classification

Primary: 30H20: Bergman spaces, Fock spaces
Secondary: 30D20: Entire functions, general theory 30C15: Zeros of polynomials, rational functions, and other analytic functions (e.g. zeros of functions with bounded Dirichlet integral) 46E22: Hilbert spaces with reproducing kernels (=
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 532 - 543
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aadi, D., Bouya, B., and Omari, Y., On zero sets in Fock spaces . J. Math. Anal. Appl. 466(2018), no. 2, 1299–1307.CrossRefGoogle Scholar
Ascensi, G., Lyubarskii, Y., and Seip, K., Phase space distribution of Gabor expansions . Appl. Comput. Harmon. Anal. 26(2009), no. 2, 277–282.CrossRefGoogle Scholar
Avdonin, S. A., On the question of Riesz bases of exponential functions in L 2 . Vestnik Leningrad Univ. Ser. Mat. 13(1974), 5–12.Google Scholar
Baranov, A., Dumont, A., Hartmann, A., and Kellay, K., Sampling, interpolation and Riesz bases in small Fock spaces . J. Math. Pures Appl. 103(2015), no. 6, 1358–1389.CrossRefGoogle Scholar
Boas, R., Entire functions, Academic Press, New York, 1954.Google Scholar
Duren, P., Theory of Hp spaces, Academic Press, New York, 1970.Google Scholar
Hedenmalm, H., Korenblum, B., and Zhu, K., Theory of Bergman spaces, Graduate texts in Mathematics, 199, Springer, New York, 2000.CrossRefGoogle Scholar
Horowitz, C., Zeros of functions in the Bergman spaces . Duke Math. J. 41(1974), no. 4, 693–710.CrossRefGoogle Scholar
Kadets, M. I., The exact value of the Paley–Wiener constant . Sov. Math. Dokl. 5(1964), 559–561.Google Scholar
Levin, B. Y., Lectures on entire functions, Translations of Mathematical Monographs, 150, American Mathematical Society, Providence, RI, 1996.CrossRefGoogle Scholar
Lyubarskii, Y., Frames in the Bargmann space of entire functions . Adv. Soviet Math. 429(1992), 107–113.Google Scholar
Lyubarskii, Y. and Seip, K., Complete interpolating sequences for Paley–Wiener spaces and Muckenhoupt’s (Ap ) condition . Rev. Mat. Iberoam. 13(1997), no. 2, 361–376.CrossRefGoogle Scholar
Mishko, M. and Wick, B. D., On the uniqueness sets in the Fock space, Preprint, 2013. arXiv:1306.0318 Google Scholar
Omari, Y., A stability problem for some complete and minimal Gabor systems in L 2 (ℝ) . Stud. Math. 254(2020), 45–75.CrossRefGoogle Scholar
Omari, Y., Complete interpolating sequences for small Fock spaces . J. Funct. Anal. 281(2021), no. 5, 109064.CrossRefGoogle Scholar
Seip, K., Density theorems for sampling and interpolation in the Bargmann–Fock space I. J. Reine Angew. Math. 1992(1992), no. 429, 91–106.Google Scholar
Zhu, K., Zeros of functions in Fock spaces . Complex Var. Elliptic Equ. 21(1993), nos. 1–2, 87–98.Google Scholar
Zhu, K., Maximal zero sequences for Fock spaces. Preprint, 2011. arXiv:1110.2247 CrossRefGoogle Scholar
Zhu, K., Analysis on Fock spaces, Graduate Texts in Mathematics, 263, Springer, New York, 2012.CrossRefGoogle Scholar