Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:46:21.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Zariski dense orbits for regular self-maps on split semiabelian varieties

Part of: Arithmetic problems. Diophantine geometry Abelian varieties and schemes

Published online by Cambridge University Press:  05 March 2021

Dragos Ghioca  and
Sina Saleh
Dragos Ghioca*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BCV6T 1Z2, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a direct proof of the Medvedev–Scanlon’s conjecture from Medvedev and Scanlon (Ann. Math. Second Series 179(2014), 81–177) regarding Zariski dense orbits under the action of regular self-maps on split semiabelian varieties defined over a field of characteristic 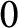$0$ . Besides obtaining significantly easier proofs than the ones previously obtained in Ghioca and Scanlon (Trans. Am. Math. Soc. 369(2017), 447–466; for the case of abelian varieties) and Ghioca and Satriano (Trans. Am. Math. Soc. 371(2019), 6341–6358; for the case of semiabelian varieties), our method allows us to exhibit numerous starting points with Zariski dense orbits, which the methods from Ghioca and Scanlon (Trans. Am. Math. Soc. 369(2017), 447–466) and Ghioca and Satriano (Trans. Am. Math. Soc. 371(2019), 6341–6358) could not provide.

Keywords

Abelian varietiesZariski dense orbitsdominant endomorphisms

MSC classification

Primary: 14K15: Arithmetic ground fields
Secondary: 14G05: Rational points
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 116 - 122
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amerik, E. and Campana, F., Fibrations méromorphes sur certaines variétés à fibré canonique trivial. Pure Appl. Math. Q. 4(2008), no. 2, Special Issue: In honor of Fedor Bogomolov. Part 1, 509–545.CrossRefGoogle Scholar
Bell, J. P., Ghioca, D., and Reichstein, Z., On a dynamical version of a theorem of Rosenlicht. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 17(2017), no. 1, 187–204.Google Scholar
Bell, J. P., Ghioca, D., Reichstein, Z., and Satriano, M., On the Medvedev–Scanlon conjecture for minimal threefolds of nonnegative Kodaira dimension. New York J. Math. 23(2017), 1185–1203.Google Scholar
Bell, J. P., Ghioca, D., and Tucker, T. J., The dynamical Mordell–Lang conjecture . Mathematical Surveys and Monographs, 210, Amer. Math. Society, Providence, RI, 2016, xiii+280 pp.CrossRefGoogle Scholar
Faltings, G., The general case of S. Lang’s conjecture . Barsotti Sympos. Algebraic Geometry (Abano Terme, 1991), Perspect. Math., 15, Academic Press, San Diego, CA, 1994, pp. 175–182.Google Scholar
Ghioca, D. and Hu, F., Density of orbits of endomorphisms of commutative linear algebraic groups. New York J. Math. 24(2018), 375–388.Google Scholar
Ghioca, D. and Satriano, M., Density of orbits of dominant regular self-maps of semiabelian varieties. Trans. Am. Math. Soc. 371(2019), no. 9, 6341–6358.10.1090/tran/7475CrossRefGoogle Scholar
Ghioca, D. and Scanlon, T., Density of orbits of endomorphisms of abelian varieties. Trans. Amer. Math. Soc. 369(2017), no. 1, 447–466.10.1090/tran6648CrossRefGoogle Scholar
Ghioca, D. and Tucker, T. J., A reformulation of the dynamical Manin–Mumford conjecture. Bull. Aus. Math. Soc. 103(2021), no. 1, 154–161.10.1017/S0004972720000477CrossRefGoogle Scholar
Ghioca, D. and Xie, J., Algebraic dynamics of skew-linear self-maps. Proc. Amer. Math. Soc. 146(2018), no. 10, 4369–4387.CrossRefGoogle Scholar
Hrushovski, E., The Mordell–Lang conjecture for function fields. J. Amer. Math. Soc. 9(1996), no. 3, 667–690.CrossRefGoogle Scholar
Laurent, M., Équations diophantiennes exponentielles. Invent. Math. 78(1984), no. 2, 299–327.CrossRefGoogle Scholar
Medvedev, A. and Scanlon, T., Invariant varieties for polynomial dynamical systems. Ann. of Math. (2) 179(2014), no. 1, 81–177.CrossRefGoogle Scholar
Noguchi, J. and Winkelmann, J., Nevanlinna theory in several complex variables and Diophantine approximation . Grundlehren der Mathematischen Wissenschaften, 350, Springer, Tokyo, 2014, xiv+416 pp.10.1007/978-4-431-54571-2CrossRefGoogle Scholar
Pink, R. and Rössler, D., On $\psi$ -invariant subvarieties of semiabelian varieties and the Manin–Mumford conjecture . J. Algebraic Geom. 13(2004), no. 4, 771–798.CrossRefGoogle Scholar
Villareal, O., Moving subvarieties by endomorphisms. Manuscripta Math. 125(2008), no. 1, 81–93.10.1007/s00229-007-0141-zCrossRefGoogle Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties I. Invent. Math. 126(1996), no. 1, 133–181.10.1007/s002220050092CrossRefGoogle Scholar
Xie, J., The existence of Zariski dense orbits for endomorphisms of projective surfaces (with an appendix in collaboration with Thomas Tucker). Preprint, 2019. arxiv:1905.07021 Google Scholar
Zhang, S., Distributions in algebraic dynamics . In: Surveys in differential geometry. Vol. X, International Press, Somerville, MA, 2006, pp. 381–430.Google Scholar