Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erbe, L. H.
and
Yan, Peng Xiang
1993.
Oscillation criteria for Hamiltonian matrix difference systems.
Proceedings of the American Mathematical Society,
Vol. 119,
Issue. 2,
p.
525.
Chen, S.-Z.
and
Erbe, L.
1994.
Oscillation results for second order scalar and matrix difference equations.
Computers & Mathematics with Applications,
Vol. 28,
Issue. 1-3,
p.
55.
Lalli, B.S.
and
Grace, S.R.
1994.
Oscillation theorems for second order neutral difference equations.
Applied Mathematics and Computation,
Vol. 62,
Issue. 1,
p.
47.
Kong, Q.
and
Zettl, A.
1995.
Interval Oscillation Conditions for Difference Equations.
SIAM Journal on Mathematical Analysis,
Vol. 26,
Issue. 4,
p.
1047.
Erbe, Lynn H.
and
Yan, Pengxiang
1995.
On the Discrete Riccati Equation and Its Applications to Discrete Hamiltonian Systems.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 1,
Kong, Qingkai
1995.
Oscillation of second order nonlinear difference equations.
Journal of Difference Equations and Applications,
Vol. 1,
Issue. 3,
p.
271.
Li, Horng-Jaan
and
Yeh, Cheh-Chih
1998.
Oscillation criteria for second-order neutral delay difference equations.
Computers & Mathematics with Applications,
Vol. 36,
Issue. 10-12,
p.
123.
Zhang, Zhenguo
and
Zhang, Jinlian
1999.
Oscillation criteria for second-order functional difference equations with “summation small” coefficient.
Computers & Mathematics with Applications,
Vol. 38,
Issue. 1,
p.
25.
Řehák, Pavel
2000.
Hartman–Wintner Type Lemma, Oscillation, and Conjugacy Criteria for Half-Linear Difference Equations.
Journal of Mathematical Analysis and Applications,
Vol. 252,
Issue. 2,
p.
813.
Shi, Yuming
2003.
Oscillation of self-adjoint second-order vector difference equations to the parameter.
Computers & Mathematics with Applications,
Vol. 45,
Issue. 10-11,
p.
1591.
El-Morshedy, Hassan A.
and
Grace, S.R.
2005.
Comparison theorems for second order nonlinear difference equations.
Journal of Mathematical Analysis and Applications,
Vol. 306,
Issue. 1,
p.
106.
2005.
Half-Linear Differential Equations.
Vol. 202,
Issue. ,
p.
471.
Hilscher, Roman
and
Zeidan, Vera
2005.
Nonnegativity and positivity of quadratic functionals in discrete calculus of variations: survey.
Journal of Difference Equations and Applications,
Vol. 11,
Issue. 9,
p.
857.
Yu, Jianshe
and
Guo, Zhiming
2006.
On boundary value problems for a discrete generalized Emden–Fowler equation.
Journal of Differential Equations,
Vol. 231,
Issue. 1,
p.
18.
Yu, Jianshe
and
Guo, Zhiming
2006.
Boundary value problems of discrete generalized Emden-Fowler equation.
Science in China Series A: Mathematics,
Vol. 49,
Issue. 10,
p.
1303.


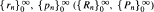 are seQuences of real numbers (
are seQuences of real numbers (