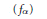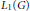Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ABDOLLAHI, A.
REJALI, A.
and
YOUSOFZADEH, A.
2009.
CONFIGURATION OF NILPOTENT GROUPS AND ISOMORPHISM.
Journal of Algebra and Its Applications,
Vol. 08,
Issue. 03,
p.
339.
Rejali, A.
and
Yousofzadeh, A.
2010.
Group Properties Characterized by Two-sided Configurations.
Algebra Colloquium,
Vol. 17,
Issue. 04,
p.
583.
YOUSOFZADEH, AKRAM
TAVAKOLI, ALI
and
REJALI, ALI
2014.
ON CONFIGURATION GRAPH AND PARADOXICAL DECOMPOSITION.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 02,
p.
1350086.
Willson, Benjamin
2014.
Configurations and invariant nets for amenable hypergroups and related algebras.
Transactions of the American Mathematical Society,
Vol. 366,
Issue. 10,
p.
5087.
Yousofzadeh, Akram
2018.
A constructive way to compute the Tarski number of a group.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 07,
p.
1850139.
Hopfensperger, John
2020.
Counting topologically invariant means on $L_\infty(G)$ and $VN(G)$ with ultrafilters.
Rocky Mountain Journal of Mathematics,
Vol. 50,
Issue. 6,
Malekan, Meisam Soleimani
and
Rejali, Ali
2020.
Two-sided configuration equivalence and isomorphism.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 10,
p.
2050189.
Hopfensperger, John
2021.
When is an invariant mean the limit of a Følner net?.
Topology and its Applications,
Vol. 300,
Issue. ,
p.
107755.
Meisami, Mahdi
Rejali, Ali
Soleimani Malekan, Meisam
and
Yousofzadeh, Akram
2022.
Locally finite groups and configurations.
Journal of Group Theory,
Vol. 25,
Issue. 1,
p.
63.
Gheisari, Elham
and
Yousofzadeh, Akram
2022.
Configurations and Paradoxical Decomposition for LAU Algebras.
Iranian Journal of Science and Technology, Transactions A: Science,
Vol. 46,
Issue. 2,
p.
637.