No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let {Xi:i=1, 2,…} be a real strictly stationary process (defined on a probability space (Ω, A, P)) which has absolutely continuous finite dimensional distributions (with respect to Lebesgue measure) and satisfies the ϕ-mixing condition: Let 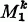 and
and 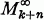 denote the sub-cr-fields generated, respectively, by {Xi:i≤k} and {Xi:i≥k+n}; then, for each k≥1 and n≥l,
denote the sub-cr-fields generated, respectively, by {Xi:i≤k} and {Xi:i≥k+n}; then, for each k≥1 and n≥l, 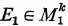 and
and 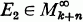 together imply.
together imply.
Supported partially by the National Research Council of Canada Grant #A-3061.