Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T01:51:59.421Z Has data issue: false hasContentIssue false
  • English
  • Français

The Verdier Hypercovering Theorem

Published online by Cambridge University Press:  20 November 2018

J. F. Jardine
J. F. Jardine*
Affiliation:
Mathematics Department, University of Western Ontario, London, ON N6A 5B7e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note gives a simple cocycle-theoretic proof of the Verdier hypercovering theorem. This theorem approximates morphisms 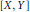$[X,\,Y]$ in the homotopy category of simplicial sheaves or presheaves by simplicial homotopy classes of maps, in the case where $Y$ is locally fibrant. The statement proved in this paper is a generalization of the standard Verdier hypercovering result in that it is pointed (in a very broad sense) and there is no requirement for the source object 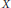$X$ to be locally fibrant.

Keywords

14F3518G3055U35simplicial presheafhypercovercocycle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 319 - 328
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Artin, M. and Mazur, B, B., Etale Homotopy. Lecture Notes in Mathematics 100, Springer-Verlag, Berlin, 1969.Google Scholar
[2] Blanc, D., Dwyer, W. G., and Goerss, P. G., The realization space of П-algebra: a moduli problem in algebraic topology. Topology 43(2004), no. 4, 857–892. http://dx.doi.org/10.1016/S0040-9383(03)00074-0 Google Scholar
[3] Brown, K. S., Abstract homotopy theory and generalized sheaf cohomology. Trans. Amer. Math. Soc. 186(1974), 419–458. http://dx.doi.org/10.1090/S0002-9947-1973-0341469-9 Google Scholar
[4] Dugger, D., Hollander, S., and Isaksen, D. C., Hypercovers and simplicial presheaves. Math. Proc. Cambridge Philos. Soc. 136(2004), no. 1, 9–51. doi=10.1017/S0305004103007175. http://dx.doi.org/10.1017/S0305004103007175 Google Scholar
[5] Dwyer, W. G. and Kan, D. M., Function complexes in homotopical algebra. Topology 19(1980), no. 4, 427–440. http://dx.doi.org/10.1016/0040-9383(80)90025-7 Google Scholar
[6] Friedlander, E. M., Étale Homotopy of Simplicial Schemes. Annals of Mathematics Studies 104. Princeton University Press, Princeton, NJ, 1982.Google Scholar
[7] Jardine, J. F., Simplicial objects in a Grothendieck topos. In: Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory, Part I. Amererican Mathematical Society, Providence, RI, 1986, 193–239.Google Scholar
[8] Jardine, J. F., Simplicial presheaves. J. Pure Appl. Algebra 47(1987), no. 1, 35–87. http://dx.doi.org/10.1016/0022-4049(87)90100-9 Google Scholar
[9] Jardine, J. F., Universal Hasse-Witt classes. In: Algebraic K-Theory and Algebraic Number Theory. Contemp. Math. 83. American Mathematical Society, Providence, RI, 1989, pp. 83–100.Google Scholar
[10] Jardine, J. F., Cocycle categories. In: Algebraic Topology 4. Springer, Berlin 2009, pp. 185–218.Google Scholar
[11] Fabien, M., and Voevodsky, V., A 1 -homotopy theory of schemes. Inst. Hautes études Sci. Publ. Math. 1999(2001), no. 90, 45–143.Google Scholar