Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T16:42:30.907Z Has data issue: false hasContentIssue false
  • English
  • Français

VB-Courant Algebroids, E-Courant Algebroids and Generalized Geometry

Published online by Cambridge University Press:  20 November 2018

Honglei Lang ,
Yunhe Sheng  and
Aïssa Wade
Honglei Lang
Affiliation:
Max Planck Institute for Mathematics, Bonn D-53111, Germany, e-mail : [email protected]
Yunhe Sheng
Affiliation:
Department of Mathematics, Jilin University, Changchun, 130012, Jilin, China, e-mail : [email protected]
Aïssa Wade
Affiliation:
Mathematics Department, Penn State University, University Park, Pennsylvania 16802, USA, e-mail : [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we first discuss the relation between 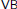$\text{VB}$-Courant algebroids and $\text{E}$-Courant algebroids, and we construct some examples of $\text{E}$-Courant algebroids. Then we introduce the notion of a generalized complex structure on an $\text{E}$-Courant algebroid, unifying the usual generalized complex structures on even-dimensional manifolds and generalized contact structures on odd-dimensional manifolds. Moreover, we study generalized complex structures on an omni-Lie algebroid in detail. In particular, we show that generalized complex structures on an omni-Lie algebra 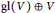$\text{gl}\left( V \right)\oplus V$ correspond to complex Lie algebra structures on 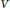$V$.

Keywords

53D1718B4058H05VB-Courant algebroidE-Courant algebroidomni-Lie algebroidgeneralized complex structurealgebroid-Nijenhuis structure
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 588 - 607
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Barton, J. and Stienon, M., Generalized complex submanifolds. Pacific J. Math. 236(2008), no. 1, 23–44. http://dx.doi.org/10.2140/pjm.2008.236.23Google Scholar
[2] Baraglia, D., Conformal Courant algebroids and orientifold T-duality. Int. J. Geom. Methods Mod. Phys. 10(2013), no. 2, 1250084. http://dx.doi.Org/10.1142/S0219887812500843Google Scholar
[3] Bursztyn, H., Cavalcanti, G., and Gualtieri, M., Reduction of Courant algebroids and generalized complex structures. Adv. Math. 211(2007), no. 2, 726–765. http://dx.doi.Org/10.1016/j.aim.2006.09.008Google Scholar
[4] Chen, Z. and Liu, Z. J., Omni-Lie algebroids. J. Geom. Phys. 60(2010), no. 5, 799–808. http://dx.doi.Org/10.1016/j.geomphys.2010.01.007Google Scholar
[5] Chen, Z., Liu, Z. J., and Sheng, Y. H., E-Courant algebroids. Int. Math. Res. Not. IMRN 2010, no. 22, 4334-4376. http://dx.doi.Org/10.1093/imrn/rnq053Google Scholar
[6] Crainic, M., Generalized complex structures and Lie brackets. Bull. Braz. Math. Soc. (N.S.) 42(2011), no. 4, 559–578. http://dx.doi.org/10.1007/s00574-011-0029-0Google Scholar
[7] Grabowski, J. and Marmo, G., The graded facobi algebras and (co)homology. J. Phys. A 36(2003), no. 2, 161–181. http://dx.doi.Org/10.1088/0305-4470/36/1/311Google Scholar
[8] Gualtieri, M., Generalized complex geometry. Ann. of Math. (2) 174(2011), no. 1, 75–123. http://dx.doi.Org/10.4007/annals.2011.174.1.3Google Scholar
[9] Hitchin, N. J., Generalized Calabi-Yau manifolds. Q. J. Math. 54(2003), no. 3, 281–308. http://dx.doi.org/10.1093/qjmath/543.281Google Scholar
[10] Iglesias-Ponte, D. and Wade, A., Contact manifold and generalized complex structures. I. Geom. Phys. 53(2005), no. 3, 249–258. http://dx.doi.Org/10.1016/j.geomphys.2004.06.006Google Scholar
[11] Jotz Lean, M., N-manifolds of degree 2 and metric double vector bundles. arxiv:1504.00880Google Scholar
[12] Kirillov, A., Local Lie algebras. Russian Math. Surveys 31(1976), 55–76. http://dx.doi.Org/10.1070/RM1976v031n04ABEH001556Google Scholar
[13] Lang, H., Sheng, Y., and Xu, X., Nonabelian omni-Lie algebras. In: Geometry of jets and fields, Banach Center Publ., 110, Polish Acad. Sei. Inst. Math., Warsaw, 2016, pp. 167–176.Google Scholar
[14] Li-Bland, D., AV-Courant algebroids and generalized CR structures. Canad. J. Math. 63(2011), no. 4, 938–960. http://dx.doi.org/10.4153/CJM-2011-009-1Google Scholar
[15] Li-Bland, D., JZ-A-Courant algebroids and their applications. Thesis, University of Toronto, 2012. arxiv:1204.2796v1Google Scholar
[16] Li-Bland, D. and Meinrenken, E., Courant algebroids and Poisson geometry. Int. Math. Res. Not. IMRN 11(2009), 2106–2145. http://dx.doi.Org/10.1093/imrn/rnp048Google Scholar
[17] Liu, Z. J., Weinstein, A., and Xu, P., Manin triplesfor Lie bialgebroids. J. Differential Geom. 45(1997), no. 3, 547–574.Google Scholar
[18] Mackenzie, K., General theories of Lie groupoids and Lie algebroids. London Mathematical Society Lecture Note Series, 213, Cambridge University Press, Cambridge, 2005. http://dx.doi.Org/10.1017/CBO9781107325883Google Scholar
[19] Mackenzie, K., Ehresmann doubles and Drindel'd doublesfor Lie algebroids and Lie bialgebroids. J. Reine Angew. Math. 658(2011), 193–245. http://dx.doi.Org/10.1515/CRELLE.2011.092Google Scholar
[20] Roytenberg, D., Courant algebroids, derived brackets and even symplectic supermanifolds. PhD thesis, University of California Berkeley, 1999. arxiv:math.DG/9910078Google Scholar
[21] Sheng, Y., On deformations of Lie algebroids. Results. Math. 62(2012), no. 1-2, 103–120. http://dx.doi.Org/10.1007/s00025-011-0133-xGoogle Scholar
[22] Stienon, M. and Xu, P., Reduction of generalized complex structures. J. Geom. Phys. 58(2008), no. 1, 105–121. http://dx.doi.Org/10.1016/j.geomphys.2007.09.009Google Scholar
[23] Vitagliano, L. and Wade, A., Generalized contact bundles. C. R. Math. Acad. Sei. Paris 354(2016), no. 3, 313–317. http://dx.doi.Org/10.1016/j.crma.2015.12.009Google Scholar
[24] Vitagliano, L. and Wade, A., Holomorphic Jacobi manifolds. arxiv:1 609.07737Google Scholar
[25] Weinstein, A., Omni-Lie algebras. Microlocal analysis ofthe Schrödinger equation and related topics. (Japanese) (Kyoto, 1999), Sürikaisekikenkyüsho Kökyüroku 1176(2000), 95–102.Google Scholar