Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-15T18:37:50.363Z Has data issue: false hasContentIssue false
  • English
  • Français

Unisolvence on Multidimensional Spaces

Published online by Cambridge University Press:  20 November 2018

Charles B. Dunham
Charles B. Dunham*
Affiliation:
University of Western Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we consider the possibility of unisolvence of a family 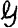of real continuous functions on a compact subset X of m-dimensional Euclidean space. Such a study is of interest for two reasons. First, an elegant theory of Chebyshev approximation has been constructed for the case where the approximating family 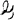is unisolvent of degree n on an interval [α, β]. We study what sort of theory results from unisolvence of degree n on a more general space. Secondly, uniqueness of best Chebyshev approximation on a general compact space to any continuous function on X can be shown if the approximating family 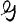is unisolvent of degree n and 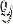satisfies certain convexity conditions. It is therefore of importance to Chebyshev approximation to consider the domains X on which unisolvence can occur. We will also study a more general condition on 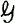involving a variable degree.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 3 , August 1968 , pp. 469 - 474
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Buck, R. C., Linear spaces and approximation theory. (In Langer, R. E. (ed.), On numerical approximation, Madison, University of Wisconsin Press, 1959). 473 Google Scholar
2. Curtis, P. C., n-parameter families and best approximation. Pacific J. Math. 9 (1959) 1013-1027.Google Scholar
3. Rice, J., Tchebycheff approximations by functions unisolvent of variable degree. Trans.Amer. Math. Soc. 99 (1961) 298-302.Google Scholar
4. Torheim, L., On n-parameter families of functions and associated convex functions. Trans. Amer. Math. Soc. 69 (1950)457-467.Google Scholar
5. Mairhuber, J., On Haar's theorem concerning Chebychev approximation problems having unique solutions. Proc. Amer. Math. Soc. 7 (1956) 609-615.Google Scholar