Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T14:40:08.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of Almost Everywhere Convergent Vilenkin Series

Published online by Cambridge University Press:  20 November 2018

W. R. Wade
W. R. Wade*
Affiliation:
Mathematics Department University of Tennessee Knoxville, Tennessee 37996 U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

D. J. Grubb [3] has shown that uniqueness holds, under a mild growth condition, for Vilenkin series which converge almost everywhere to zero. We show that, under even less restrictive growth conditions, one can replace the limit function 0 by an arbitrary 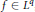$f\,\in \,{{L}^{q}}$, when 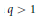$q\,>\,1$.

Keywords

43A7542C10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 3 , 01 September 2004 , pp. 475 - 480
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bokaev, N. A. and Skvortsov, V. A., A generalization of a uniqueness theorem for series in multiplicative systems. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 1987, 11–15.Google Scholar
[2] Daly, J. E. and Phillips, K. L., A note on H1 multipliers for locally compact Vilenkin groups. Canad. Math. Bull. 41 (1998), 392–397.Google Scholar
[3] Grubb, D. J., Sets of uniqueness in compact 0-dimensional metric groups Trans. Amer.Math. Soc. 301(1987) 239–249.Google Scholar
[4] Vilenkin, N. Ya., On a class of complete orthonormal systems. Izv. Akad. Nauk. SSSR, Ser.Mat. 11 (1947), 363–400.Google Scholar
[5] Wade, W. R., The bounded convergence theorem. Amer.Math. Monthly 81 (1974), 387–389.Google Scholar