Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T02:16:44.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness Implies Existence and Uniqueness Conditions for a Class of (k + j)-Point Boundary Value Problems for n-th Order Differential Equations

Published online by Cambridge University Press:  20 November 2018

Paul W. Eloe ,
Johnny Henderson  and
Rahmat Ali Khan
Paul W. Eloe
Affiliation:
Department of Mathematics, University of Dayton, Dayton, OH, 45469-2316, USAe-mail: [email protected]
Johnny Henderson
Affiliation:
Department of Mathematics, Baylor University, Waco, TX, 76798-7328, USAe-mail: Johnny [email protected]
Rahmat Ali Khan
Affiliation:
Centre for Advanced Mathematics and Physics, National University of Sciences and Technology(NUST), Campus of College of Electrical and Mechanical Engineering, Peshawar Road, Rawalpindi, Pakistane-mail: rahmat [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the $n$-th order nonlinear differential equation, 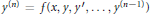${{y}^{(n)}}\,=\,f(x,\,y,\,y\prime ,\ldots ,\,{{y}^{(n-1)}})$, we consider uniqueness implies uniqueness and existence results for solutions satisfying certain 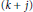$(k\,+\,j)$-point boundary conditions for 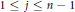$1\,\le \,j\,\le \,n\,-\,1$ and 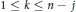$1\,\le \,k\,\le \,n\,-\,j$. We define 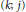$(k;\,j)$-point unique solvability in analogy to $k$-point disconjugacy and we show that 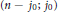$(n\,-\,{{j}_{0}};\,{{j}_{0}})$-point unique solvability implies 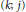$(k;\,j)$-point unique solvability for 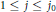$1\,\le \,j\,\le \,{{j}_{0}}$, and 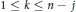$1\,\le \,k\,\le \,n\,-\,j$. This result is analogous to $n$-point disconjugacy implies $k$-point disconjugacy for 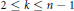$2\,\le \,k\,\le \,n\,-\,1$.

Keywords

34B1534B1065D05boundary value problemuniquenessexistenceunique solvabilitynonlinear interpolation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 285 - 296
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Clark, S. and Henderson, J., Uniqueness implies existence and uniqueness criterion for nonlocal boundary value problems for third order differential equations. Proc. Amer. Math. Soc. 134(2006), 3363–3372. http://dx.doi.org/10.1090/S0002-9939-06-08368-7 Google Scholar
[2] Ehme, J. and Hankerson, D., Existence of solutions for right focal boundary value problems. Nonlinear Anal. 18(1992), no. 2, 191–197. http://dx.doi.org/10.1016/0362-546X(92)90093-T Google Scholar
[3] Eloe, P. W. and Henderson, J., Uniqueness implies existence and uniqueness conditions for nonlocal boundary value problems for nth order differential equations. J. Math. Anal. Appl. 331(2007), no. 1, 240–247. http://dx.doi.org/10.1016/j.jmaa.2006.08.087 Google Scholar
[4] Gray, M., Uniqueness implies uniqueness and existence for nonlocal boundary value problems for third order ordinary differential equations. Comm. Appl. Nonlinear Anal. 13(2006), no. 4, 19–30.Google Scholar
[5] Harris, G. A., Henderson, J., Lanz, A., and Yin, W. K. C., Third order right focal boundary value problems on a time scale. J. Difference Equ. Appl. 12(2006), no. 6, 525–533. http://dx.doi.org/10.1080/10236190500539212 Google Scholar
[6] Hartman, P., Unrestricted n-parameter families. Rend. Circ. Mat. Palermo 7(1958), 123–142. http://dx.doi.org/10.1007/BF02854523 Google Scholar
[7] Hartman, P., On N-parameter families and interpolation problems for nonlinear differential equations. Trans. Amer. Math. Soc. 154(1971), 201–226.Google Scholar
[8] Henderson, J., Uniqueness of solutions of right focal point boundary value problems. J. Differential Equations 41(1981), no. 2, 218–227. http://dx.doi.org/10.1016/0022-0396(81)90058-9 Google Scholar
[9] Henderson, J., Existence of solutions of right focal point boundary value problems for ordinary differential equations. Nonlinear Anal. 5(1981), no. 9, 989–1002. http://dx.doi.org/10.1016/0362-546X(81)90058-4 Google Scholar
[10] Henderson, J., Existence theorems for boundary value problems for nth order nonlinear difference equations. SIAM J. Math. Anal. 20(1989), no. 2, 468–478. http://dx.doi.org/10.1137/0520032 Google Scholar
[11] Henderson, J., Focal boundary value problems for nonlinear difference equations. I, II. J. Math. Anal. Appl. 141(1989), 559–567, 568-579. http://dx.doi.org/10.1016/0022-247X(89)90197-2 Google Scholar
[12] Henderson, J., Karna, B., and Tisdell, C. C., Existence of solutions for three-point boundary value problems for second order equations. Proc. Amer. Math. Soc. 133(2005), no. 5, 1365–1369. http://dx.doi.org/10.1090/S0002-9939-04-07647-6 Google Scholar
[13] Henderson, J. and Ma, D., Uniqueness of solutions for fourth order nonlocal boundary value problems. Bound. Value Probl. 2006, Art. ID 23875.Google Scholar
[14] Henderson, J. and Yin, W. K. C., Existence of solutions for fourth order boundary value problems on a time scale. J. Difference Equ. Appl. 9(2003), no. 1, 15–28.Google Scholar
[15] Jackson, L. K., Uniqueness of solutions of boundary value problems for ordinary differential equations. SIAM J. Appl. Math. 24(1973), 525–538. http://dx.doi.org/10.1137/0124054 Google Scholar
[16] Jackson, L. K., Existence and uniqueness of solutions for third order differential equations. J. Differential Equations 13(1973), 432–437. http://dx.doi.org/10.1016/0022-0396(73)90002-8 Google Scholar
[17] Jones, G. D., Existence of solutions of multipoint boundary value problems for a second order differential equation. Dynam. Systems Appl. 16(2007), no. 4, 709–711.Google Scholar
[18] Klaasen, G., Existence theorems for boundary value problems of nth order ordinary differential equations. Rocky Mtn. J. Math. 3(1973), 457–472. http://dx.doi.org/10.1216/RMJ-1973-3-3-457 Google Scholar
[19] Lasota, A. and Opial, Z., On the existence and uniqueness of solutions of a boundary value problem for an ordinary second order differential equation. Colloq. Math. 18(1967), 1–5.Google Scholar
[20] Peterson, A. C., Existence-uniqueness for focal-point boundary value problems. SIAM J. Math. Anal. 12(1982), no. 2, 173–185. http://dx.doi.org/10.1137/0512018 Google Scholar
[21] Schrader, K., Uniqueness implies existence for solutions of nonlinear boundary value problems. Abstracts Amer. Math. Soc. 6(1985), 235.Google Scholar
[22] Spanier, E. H., Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar