Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T16:30:48.746Z Has data issue: false hasContentIssue false
  • English
  • Français

Une classe d’hamiltoniens polynomiaux isochrones

Published online by Cambridge University Press:  20 November 2018

Bertrand Schuman
Bertrand Schuman*
Affiliation:
Université Pierre etMarie Curie, Paris 6, Tour 46-0, 5ème étage, case 172 4, place Jussieu 75252 Paris Cedex 05 France, courriel: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit 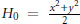${{H}_{0}}\,=\,\frac{{{x}^{2}}+{{y}^{2}}}{2}$ un hamiltonien isochrone du plan 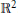${{\mathbb{R}}^{2}}$. On met en évidence une classe d’hamiltoniens isochrones qui sont des perturbations polynomiales de 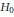${{H}_{0}}$. On obtient alors une condition nécessaire d’isochronisme, et un critère de choix pour les hamiltoniens isochrones. On voit ce résultat comme étant une généralisation du caractère isochrone des perturbations hamiltoniennes homogènes considérées dans 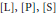$\left[ \text{L} \right],\,\left[ \text{P} \right],\,\left[ \text{S} \right]$.

Abstract

Abstract

Let 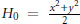${{H}_{0}}\,=\,\frac{{{x}^{2}}+{{y}^{2}}}{2}$ be an isochronous Hamiltonian of the plane 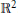${{\mathbb{R}}^{2}}$. We obtain a necessary condition for a system to be isochronous. We can think of this result as a generalization of the isochronous behaviour of the homogeneous polynomial perturbation of the Hamiltonian 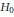${{H}_{0}}$ considered in 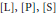$\left[ \text{L} \right],\,\left[ \text{P} \right],\,\left[ \text{S} \right]$.

Keywords

34C2058F0558F2258F30Hamiltonian systemnormal formsresonancelinearization
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 323 - 334
Copyright
Copyright © Canadian Mathematical Society 2001

References

[A1] Arnold, V. I., Dynamical systems III. Encyclopaedia Math. Sci. Vol. 3, Springer Verlag, 1988.Google Scholar
[A2] Arnold, V. I., Geometrical methods in the theory of ordinary differential equations. Grundlehren Math. Wiss. 250, Springer-Verlag, 1988; Chapitres supplémentaires de la théorie des équations différentielles ordinaires. Mir, Moscou, 1980.Google Scholar
[B] Birkhoff, G. D., Dynamical systems. Amer. Math. Soc. Colloq. Publ. IX, 1927.Google Scholar
[Ch.D] Christopher, C.-J. and Devlin, J., Isochronous centers in planar polynomial systems. SIAM J. Math. Anal. 28 (1997), 162–177.Google Scholar
[F1] Franc¸oise, J.-P., Birkhoff normal forms and analytic geometry. Dans: Symplectic singularities and geometry of gauge fields, Banach Center Publ. 39, Polish Acad. Sci., Warszawa, 1997, 49–56.Google Scholar
[F2] Françoise, J.-P., The successive derivatives of the period function of a plane vector field. J. Differential Equations 146 (1998), 320–335.Google Scholar
[G] Gavrilov, L., Isochronicity of plane polynomial Hamiltonian systems. Nonlinearity 10 (1997), 433–448.Google Scholar
[L] Loud, W. S., Behaviour of the period of solutions of certain plane autonomous systems near centers. Contributions to Differential Equations 3 (1964), 21–36.Google Scholar
[P] Pleshkan, I. I., A new method of investigating the isochronicity of a system of two differential equations. Differential Equations 5 (1969), 796–802.Google Scholar
[R.T1] Rousseau, C. and Toni, B., Local bifurcation of critical periods in vector fields with homogeneous nonlinearities of the third degree. Canad. Math. Bull. (4) 36 (1993), 473–484.Google Scholar
[R.T2] Rousseau, C. and Toni, B., Local bifurcation of critical periods in the reduced Kukles system. Canad. J. Math. (2) 49 (1997), 338–358.Google Scholar
[S] Schuman, B., Sur la forme normale de Birkhoff et les centres isochrones. C. R. Acad. Sci. Paris Sér. I 322 (1996), 21–24.Google Scholar