Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-08T17:49:13.850Z Has data issue: false hasContentIssue false
  • English
  • Français

Une Application de la Theorie de Ltnterpolation-(0,2)

Published online by Cambridge University Press:  20 November 2018

C. Côté  and
R. Gervais
C. Côté
Affiliation:
Département de Mathématiques, Université de Montréal, MontréalQuébec, Canada
R. Gervais
Affiliation:
Département de Mathématiques, Université de Montréal, MontréalQuébec, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Donné (n + 2) points dans l'intervalle [-1,1],

1.1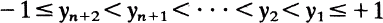

L. Fejér a montré ([3]) qu'il existe toujours un polynôme 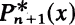de degré inférieur ou égal à n + 1 tel que

1.2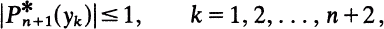

et

1.3

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 1 , 01 March 1977 , pp. 53 - 66
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Cheney, E. W., Introduction to Approximation Theory, McGraw-Hill. (1966).Google Scholar
2. Duffin, R. J. and Schaeffer, A. C., A refinement of an inequality of the brothers Markoff, Trans. Amer. Math. Soc. 50, (1941) 517-528.Google Scholar
3. Fejer, L., Die abschátzung eines polynoms in einem intervalle…, Math. Zeitschrift, 32 (1930), 426-457.Google Scholar
4. Rahman, Q. I., On a problem of Turán about polynomials with curved majorants, Trans. Amer. Math. Soc. 163 (1972), 447-455.Google Scholar
5. Szego, G., Orthogonal Polynomials (3e ed. 1974), Amer. Math. Soc. Coll. Publ., 23, 348.Google Scholar