Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T12:21:07.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Triples and Localizations(1)

Published online by Cambridge University Press:  20 November 2018

A. G. Heinicke
A. G. Heinicke*
Affiliation:
University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a ring (associative) with unity, and let denote the category of unital left A-modules. If 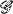is a strongly complete Serre class in then (see [3], and also [6]) there is an exact functor S: 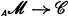, where is the quotient category 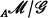, and is an abelian category.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 3 , September 1971 , pp. 333 - 339
Copyright
Copyright © Canadian Mathematical Society 1971

Footnotes

(1)

This work was partially supported by the National Research Council of Canada.

References

1. Dickson, S. E., A torsion theory for abelian categories, Trans. Amer. Math. Soc, 121 (1966), 123-235.Google Scholar
2. Eilenberg, S. and Moore, J. C., Adjoint functors and triples, Illinois J. Math. 9 (1965), 381-398.Google Scholar
3. Gabriel, P., Des categories abeliennes, Bull. Soc. Math., France, 90 (1962), 323-448.Google Scholar
4. Goldman, O., Rings and modules of quotients, J. Algebra, 13 (1969), 10-47.Google Scholar
5. Mitchell, B., Theory of categories, Academic Press, New York, 1965.Google Scholar
6. Walker, C. L. and Walker, E. A., Quotient categories and rings of quotients (to appear).Google Scholar