Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T06:06:35.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Triangulated Equivalences Involving Gorenstein Projective Modules

Published online by Cambridge University Press:  20 November 2018

Yuefei Zheng  and
Zhaoyong Huang
Yuefei Zheng
Affiliation:
Department of Applied Mathematics, College of Science, Northwest A&F University, Yangling 712100, Shaanxi Province, China e-mail: [email protected]
Zhaoyong Huang
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, Jiangsu Province, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any ring $R$, we show that, in the bounded derived category 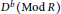${{D}^{b}}(\text{Mod}\,R)$ of left $R$-modules, the subcategory of complexes with finite Gorenstein projective (resp. injective) dimension modulo the subcategory of complexes with finite projective (resp. injective) dimension is equivalent to the stable category $\underline{\text{GP}}(\text{Mod}\,R)\,(resp.\overline{GI}(Mod\,R))$ of Gorenstein projective (resp. injective) modules. As a consequence, we get that if $R$ is a left and right noetherian ring admitting a dualizing complex, then 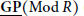$\underline{\text{GP}}(\text{Mod}\,R)$ and 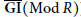$\overline{\text{GI}}(\text{Mod}\,R)$ are equivalent.

Keywords

18G2516E35triangulated equivalenceGorenstein projective modulestable categoryderived categoryhomotopy category
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 879 - 890
Copyright
Copyright © Canadian Mathematical Society 2017

References

[AI] Aihara, T. and O. Iyama, Silting mutation in triangulated categories. J. Lond. Math. Soc. 85(2012), no. 3, 633-668. http://dx.doi.org/10.1112/jlms/jdrO55 Google Scholar
[AS] Asadollahi, J. and S. Salarian, Gorenstein injective dimension for complexes and Iwanaga-Gorenstein rings. Comm. Algebra 34(2006), no. 8, 3009-3022. http://dx.doi.org/10.1080/00927870600639815 Google Scholar
[AuB] Auslander, M. and M. Bridger, Stable module theory. Memoirs of the American Mathematical Society, 94, American Mathematical Society, Providence, RI, 1969. Google Scholar
[AvF] Avramov, L. L. and H.-B. Foxby, Ring homomorphisms and finite Gorenstein dimension. Proc. London Math. Soc. 75(1997), 241-270. http://dx.doi.org/10.1112/S0024611 597000348 Google Scholar
[BR] Beligiannis, A. and I. Reiten, Homological and homotopical aspects of torsion theories. Mem. Amer. Math. Soc. 188(2007), no. 883. http://dx.doi.org/10.1090/memo/0883 Google Scholar
[Bu] Buchweitz, R. O., Maximal Cohen-Macaulay modules and Tate cohomology over Gorenstein rings. Unpublished manuscript, 1986. https://tspace.library.utoronto.ca/handle/1 807/1 6682 Google Scholar
[DEH] Dalezios, G., S. Estrada, and H. Holm, Quillen equivalences for stable categories. arxiv:1 610.02073 Google Scholar
[EJ1] Enochs, E. E. and G. Jenda, O. M., Gorenstein injective andprojective modules. Math. Z. 220(1995), no. 4, 611-633. http://dx.doi.org/10.1007/BF02572634 Google Scholar
[EJ2] Enochs, E. E. and G. Jenda, O. M., Relative homological algebra. Vol. 1. de Gruyter Expositions in Mathematics, 30, Walter de Gruyter GmbH & Co. KG, Berlin, 2011. Google Scholar
[GM] Gelfand, S. I. and Manin, Y. I., Methods of homological algebra. Second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[HI] Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras. London Mathematical Society Lecture Note Series, 119, Cambridge University Press, Cambridge, 1988. http://dx.doi.org/10.1017/CBO9780511629228 Google Scholar
[H2] Happel, D., On Gorenstein algebras. In: Representation theory of finite groups and finite-dimensional algebras (Bielefeld, 1991), Progress in Mathematics, 95, Birkhauser, Basel, 1991, pp. 389-404. http://dx.doi.org/10.1 007/978-3-0348-8658-1J 6 Google Scholar
[Ho] Holm, H., Gorenstein homological dimensions. J. Pure Appl. Algebra 189(2004), no. 1-3,167-193. http://dx.doi.org/1 0.101 6/j.jpaa.2003.11.007 Google Scholar
[IK] Iyengar, S. and H. Krause, Acyclicity versus total acyclicity for complexes over Noetherian rings. Doc. Math. 11(2006), 207-240. Google Scholar
[IYa] Iyama, O. and D. Yang, Silting reduction and Calabi-Yau reduction of triangulated categories. Trans. Amer. Math. Soc, to appear. arxiv:1408.2678Google Scholar
[IYo] Iyama, O. and Y. Yoshino, Mutations in triangulated categories and rigid Cohen-Macaulay modules. Invent. Math. 172(2008), 117-168. http://dx.doi.org/10.1007/s00222-007-0096-4 Google Scholar
[Q] Quillen, D., Higher algebraic K-theoryl. In: Algebraic Jf-theory, I: Higher Jf-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), Lecture Notes in Math., 341, Springer, Berlin, 1973, pp. 85-147. Google Scholar
[V] Veliche, O., Gorenstein protective dimension for complexes. Trans. Amer. Math. Soc. 358(2006), 1257-1283. http://dx.doi.org/10.1090/S0002-9947-05-03771 -2 Google Scholar
[Y] Yekutieli, A., Dualizing complexes over noncommutative graded algebras. J. Algebra 153(1992), 41-84. http://dx.doi.org/! 0.101 6/0021-8693(92)90148-F Google Scholar