Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-10T23:19:34.251Z Has data issue: false hasContentIssue false
  • English
  • Français

Transformation Formulas for Bilinear Sums of Basic Hypergeometric Series

Published online by Cambridge University Press:  20 November 2018

Yasushi Kajihara
Yasushi Kajihara*
Affiliation:
Department of Mathematics, Kobe University, Rokko-dai, Kobe 657-8501, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A master formula of transformation formulas for bilinear sums of basic hypergeometric series is proposed. It is obtained from the author’s previous results on a transformation formula for Milne’s multivariate generalization of basic hypergeometric series of type $A$ with different dimensions and it can be considered as a generalization of the Whipple–Sears transformation formula for terminating balanced 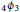$_{4}{{\phi }_{3}}$ series. As an application of the master formula, the one-variable cases of some transformation formulas for bilinear sums of basic hypergeometric series are given as examples. The bilinear transformation formulas seem to be new in the literature, even in the one-variable case.

Keywords

33D20bilinear sumsbasic hypergeometric series
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 136 - 143
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Askey, R., Orthogonal polynomials and special functions. Society for Industrial and Applied Mathematics, Philadelphia, PA, 1975.Google Scholar
[2] Andrews, G. E. and Askey, R.. Classical orthogonal polynomials. In: Orthogonal polynomials and applications (Bar-le-Duc, 1984), Lecture Notes in Math., 1171, Springer, Berlin, 1985, pp. 36–62.Google Scholar
[3] Askey, R. and Wilson, J.. Some basic hyper geometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Amer. Math. Soc. 54(1985), no. 319.Google Scholar
[4] Gasper, G. and Rahman, M.. Basic hypergeometric series. Second éd., Encyclopedia of Mathematics and its Applications, 96, Cambridge University Press, Cambridge, 2004.Google Scholar
[5] H. Ismail, M. E. and Stanton, D.. Classical orthogonal polynomials as moments. Canad. J. Math. 49(1997), no. 3, 520–542. http://dx.doi.Org/10.4153/CJM-1997-024-9 Google Scholar
[6] H. Ismail, M. E. and Stanton, D., q-integral and moment representations for q-orthogonal polynomials. Canad. J. Math. 54(2002), no. 4, 709–735. http://dx.doi.Org/10.4153/CJM-2002-027-2 Google Scholar
[7] Kajihara, Y., Some remarks on multiple Sears transformation formula. In: q-series with applications to combinatorics, number theory, and physics (Urbana, IL, 2000), Contemp. Math., 291, American Mathematical Society, Providence, RI, 2001, pp. 139–145.Google Scholar
[8] Kajihara, Y., Euler transformation formula for multiple basic hypergeometric series of type A and some applications. Adv. Math. 187(2004), no. 1, 53–97. http://dx.doi.Org/10.1016/j.aim.2003.08.012 Google Scholar
[9] Kajihara, Y., Multiple generalizations ofq-series identities and related formulas. In: Partitions, q-series and modular forms Dev. Math., 23, Springer, New York, 2012, pp. 159–180.Google Scholar
[10] Kajihara, Y., Multiple basic hypergeometric transformation formulas arising from the balanced duality transformation. arxiv:1310.1984Google Scholar
[11] Kajihara, Y., Symmetry groups of An hypergeometric series. SIGMA Symmetry Integrability Geom. Methods Appl. 10(2014), no. 026.Google Scholar
[12] Kajihara, Y and Noumi, M.. Multiple elliptic hypergeometric series. An approach from the Cauchy determinant. Indag. Math. (N.S.) 14(2003), no. 3-4, 395–421. http://dx.doi.Org/10.1016/S0019-3577(03)90054-1 Google Scholar
[13] Koelink, H. T. and J. Van der Jeugt, Convolution for orthogonal polynomials from quantum algebra representations. SIAM J. Math. Anal. 29(1998), no. 3, 794–822. http://dx.doi.Org/1 0.1137/S003614109630673X Google Scholar
[14] Labelle, J., Tableau dAskey. In: Polynômes orthogonaux et applications (Bar-le-Duc, 1984), Lecture Notes in Math., 1171, Springer-Verlag, Berlin, 1985, pp. xxxvi–xxxvii.Google Scholar
[15] Milne, S. C., A q-analogue of hypergeometric series well-poised in SU(n) and invariant G-functions. Adv. in Math. 58(1985), no. 1,1-60. http://dx.doi.Org/10.1016/0001 -8708(85)90048-9 Google Scholar
[16] Milne, S. C., Basic hypergeometric series very well-poised in U(«). J. Math. Anal. Appl. 122(1987), no. 1, 223–256. http://dx.doi.Org/10.1016/0022-247X(87)90355-6 Google Scholar
[17] Noumi, M. and Mimachi, K.. Askey- Wilson polynomials and the quantum group SUq(2). Proc. Japan Acad. Ser. A Math. Sci. 66(1990), no. 6,146-149. http://dx.doi.Org/10.3792/pjaa.66.146 Google Scholar
[18] Rahman, M., Reproducing kernels and bilinear sums for q-Racah and q-Wilson polynomials Trans. Amer. Math. Soc. 273(1982), no. 2, 483–508.Google Scholar
[19] Rahman, M., A q-extension of a product formula of Watson. Quaest. Math. 22(1999), no. 1,17-42. http://dx.doi.Org/! 0.1080/1 6073606.1 999.9632057 Google Scholar