Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T02:05:34.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Transcendental Solutions of a Class of Minimal Functional Equations

Published online by Cambridge University Press:  20 November 2018

Michael Coons
Michael Coons*
Affiliation:
University of Waterloo, Dept. of Pure Mathematics, Waterloo, ON, N2L 3G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a result concerning power series 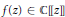$f\left( Z \right)\,\in \,\mathbb{C}\left[\!\left[ Z \right]\!\right]$ satisfying a functional equation of the form?

1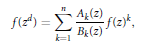

$$f\left( {{Z}^{d}} \right)\,=\,\sum\limits_{k=1}^{n}{\frac{{{A}_{k}}\left( Z \right)}{{{B}_{k}}\left( Z \right)}\,f{{\left( Z \right)}^{k}}},$$
,

where 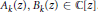${{A}_{k}}\left( Z \right),\,{{B}_{k}}\left( Z \right)\,\in \,\mathbb{C}\left[ Z \right]$. In particular, we show that if 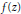$f\left( Z \right)$ satisfies a minimal functional equation of the above form with 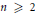$n\,\ge \,2$, then 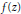$f\left( Z \right)$ is necessarily transcendental. Towards a more complete classification, the case 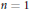$n=\,1$ is also considered.

Keywords

11B3711B8311J91transcendencegenerating functionsMahler-type functional equation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 283 - 291
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Adamczewski, B., Non-converging continued fractions related to the Stern diatomic sequence. Acta Arith. 142(2010), no. 1, 67–78. http://dx.doi.org/10.4064/aa142-1-6 Google Scholar
[2] Coons, M., The transcendence of series related to Stern's diatomic sequence. Int. J. Number Theory 6(2010), no.1, 211–217. http://dx.doi.org/10.1142/S1793042110002958 Google Scholar
[3] Coons, M., Extension of some theorems of W. Schwarz. Canad. Math. Bull. Published online March 10, 2011 http://dx.doi.org/10.4153/CMB-2011-037-9 Google Scholar
[4] Dekking, M., Transcendance du nombre de Thue-Morse. C. R. Acad. Sci. Paris Sér. A-B 285(1977), no. 4, A157–A160.Google Scholar
[5] Dilcher, K. and Stolarsky, K. B., A polynomial analogue to the Stern sequence. Int. J. Number Theory 3(2007), no. 1, 85–103. http://dx.doi.org/10.1142/S179304210700081X Google Scholar
[6] Dilcher, K. and Stolarsky, K. B., Stern polynomials and double-limit continued fractions. Acta Arith. 140(2009), no. 2, 119–134. http://dx.doi.org/10.4064/aa140-2-2 Google Scholar
[7] Golomb, S.W., On the sum of the reciprocals of the Fermat numbers and related irrationalities. Canad. J. Math. 15(1963), 475–478. http://dx.doi.org/10.4153/CJM-1963-051-0 Google Scholar
[8] Mahler, K., Arithmetische Eigenschaften der L¨osungen einer Klasse von Funktionalgleichungen. Math. Ann. 101(1929), no. 1, 342–366. http://dx.doi.org/10.1007/BF01454845 Google Scholar
[9] Mahler, K., Arithmetische Eigenschaften einer Klasse transzendental-transzendenter Funktionen. Math. Zeit. 32(1930), no. 1, 545–585. http://dx.doi.org/10.1007/BF01194652 Google Scholar
[10] Mahler, K., Über das Verschwinden von Potenzreihen mehrerer Vera¨nderlicher in speziellen Punktfolgen. Math. Ann. 103(1930), no. 1, 573–587. http://dx.doi.org/10.1007/BF01455711 Google Scholar
[11] Mahler, K., Remarks on a paper by W. Schwarz. J. Number Theory 1(1969), 512–521. http://dx.doi.org/10.1016/0022-314X(69)90013-4 Google Scholar
[12] Nishioka, K., Algebraic function solutions of a certain class of functional equations. Arch. Math. 44(1985), no. 4, 330–335. Google Scholar
[13] Schwarz, W., Remarks on the irrationality and transcendence of certain series. Math. Scand 20(1967), 269–274. Google Scholar