Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T02:24:41.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Traceless Maps as the Singular Minimizers in the Multi-dimensional Calculus of Variations

Published online by Cambridge University Press:  20 November 2018

M. S. Shahrokhi-Dehkordi
M. S. Shahrokhi-Dehkordi*
Affiliation:
Department of Mathematics, University of Shahid Beheshti, Evin, Tehran, Iran. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 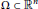$\Omega \subset {{\mathbb{R}}^{n}}$ be a bounded Lipschitz domain and consider the energy functional

1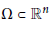

$$F[u,\Omega ]\,:=\,\,{{\int }_{\Omega }}\text{F}(\triangledown u(x))\,d\text{x,}$$

over the space of 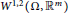${{W}^{1,2}}(\Omega ,{{\mathbb{R}}^{m}})$ where the integrand 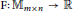$\text{F}:{{\mathbb{M}}_{m\times n}}\to \mathbb{R}$ is a smooth uniformly convex function with bounded second derivatives. In this paper we address the question of regularity for solutions of the corresponding system of Euler–Lagrange equations. In particular, we introduce a class of singularmaps referred to as traceless and examine themas a new counterexample to the regularity of minimizers of the energy functional 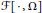$F[\cdot ,\Omega ]$ using a method based on null Lagrangians.

Keywords

49K2749N6049J3049K20traceless mapsingular minimizernull-Lagrangian
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 3 , 01 September 2017 , pp. 631 - 640
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Ball, J. M., Currie, J. C., Olver, P. J., Null Lagrangians, weak continuity, and variational problems ofarbitrary order. J. Funct. Anal. 41(1981), 135–174. http://dx.doi.Org/10.1016/0022-1236(81 )9OO85-9 Google Scholar
[2] Dacorogna, B., Direct methods in the calculus of variations. Second ed., Applied Mathematical Sciences, 78, Springer, New York, 2007. Google Scholar
[3] De Giorgi, E., Sulla differenziabilita e 1'analitia della estremali degli integrali multipli regolari. Mem. Acad. Sci. Torino Cl. Sci. Fis. Math. Nat. 3(1957), 25–43.Google Scholar
[4] De Giorgi, E., Un esempio di estremali discontinue per un problema variazionale di tipo ellittico. Boll. Un. Mat. Ital. 1(1968), 135–137. Google Scholar
[5] Evans, L. C., Quasiconvexity and partial regularity in the calculus of variations. Arch. Rational Mech. Anal 95(1984), 227–252. http://dx.doi.Org/10.1007/BF00251360 Google Scholar
[6] Fulton, W., Young tableaux: with applications to representation theory and geometry. London Mathematical Society Student Texts, 35, Cambridge University Press, Cambridge, 1997. Google Scholar
[7] Fulton, W. and Harris, J., Representation theory: a first course. Graduate Texts in Mathematics, 129, Springer-Verlag, New York, 1991. http://dx.doi.Org/10.1007/978-1 -4612-0979-9 Google Scholar
[8] Hao, W., Leonardi, S., and Necas, J., An example of irregular solution to a nonlinear Euler-Lagrange elliptic system with real analytic coefficients. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 23(1996), no. 1, 57–67.Google Scholar
[9] Kristensen, J. and Taheri, A., Partial regularity of strong local minimizers in the multi-dimensional calculus of variations. Arch. Ration. Mech. Anal. 170(2003), 63–89. http://dx.doi.Org/10.1007/s00205-003-0275-4 Google Scholar
[10] Morrey, C. B., Multiple integrals in the calculus of variations. Die Grundlehren der mathematischen Wissenschaften, 130, Springer-Verlag, New York, 1966. Google Scholar
[11] Nash, J., Continuity of solutions of parabolic and elliptic equations. Amer. J. Math. 80(1958), 931–954. http://dx.doi.Org/10.2307/2372841 Google Scholar
[12] Necas, J., Example of an irregular solution to a nonlinear elliptic system with analytic coefficients and conditions of regularity. In: Theory of nonlinear operators (Proc. Fourth Internat. Summer School, Acad. Sci., Berlin), Akademie-Verlag, Berlin, 1977, pp. 1497–206. Google Scholar
[13] Olver, P. J. and J. Sivaloganathan, The structure of null Lagrangians. Nonlinearity 1(1988), no. 2, 389–398. http://dx.doi.Org/10.1 088/0951 -771 5/1/2/005 Google Scholar
[14] Phelps, R. R., Convex functions, monotone operators and differentiability. Lecture Notes in Mathematics, 1364, Springer-Verlag, Berlin, 1993. Google Scholar
[15] Rockafellar, R. T., Convex analysis. Princeton Mathematical Series, 28, Princeton University Press, Princeton, 1970. Google Scholar
[16] Sverak, V. and Yan, X., A singular minimizer of a smooth strongly convex functional in three dimensions. Cal. Var. Partial Differential Equation 10(2000), no. 3, 213–221. http://dx.doi.Org/10.1007/s005260050151 Google Scholar
[17] Sverak, V. and Yan, X., Non-Lipschitz minimizers of smooth uniformly convex functionals. Proc. Natl. Acad. Sci. USA 99(2002), no. 24, 15269–15276. http://dx.doi.Org/10.1073/pnas.222494699 Google Scholar