Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T15:59:05.528Z Has data issue: false hasContentIssue false
  • English
  • Français

Trace Classes and Quadratic Forms in the Modular Group

Published online by Cambridge University Press:  20 November 2018

Benjamin Fine
Benjamin Fine*
Affiliation:
Department of Mathematics, Fairfield University Fairfield, Connecticut 06430 U.S.A
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Modular Group M is PSL2(Z) the group of linear fractional transformations with integral entries and determinant one. M has been of great interest in many diverse fields of Mathematics, including Number Theory, Automorphic Function Theory and Group Theory. In this paper we give an effective algorithm to determine, for each integer d, a complete set of representatives for the trace classes in trace d. This algorithm depends on the combinatorial group theoretic structure of M. It has been subsequently extended by Sheingorn to the general Hecke groups. The number h(d) of trace classes in trace d is equal to the ideal class number of the field 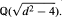The algorithm mentioned above then provides a new straightforward computational procedure for determining h(d). Finally as an outgrowth of the algorithm we present a wide generalization of the Fermat Two-Square theorem. This last result can also be derived from classical work of Gauss.

Keywords

11F0620H0511E08modular grouptrace classquadratic form
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 2 , 01 June 1994 , pp. 202 - 212
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Buell, D. A., Binary Quadratic Forms, Springer-Verlag, 1989.Google Scholar
2. Cohn, H., A Second Course in Number Theory, John Wiley, New York, 1962.Google Scholar
3. Fine, B., The Algebraic Theory of the Bianchi Groups, Marcel Dekker, 1990.Google Scholar
4. Fine, B., A Note on the Fermât Two-Square Theorem, Canad. Math. Bull. (1) 20(1977), 93–95.Google Scholar
5. Fine, B., Sum of Squares Rings, Canad. J. Math. XXIX(1977), 155–161.Google Scholar
6. Fine, B., Cyclotomic Equations and Square Properties in Rings, Internat. J. Math. (1) 9(1986), 89–95.Google Scholar
7. Fine, B., Subgroup Presentations without Coset Representatives. In: Combinatorial Group Theory, Proceedings of the Fall Foliage Conference, Springer-Verlag, 1990,59–74.Google Scholar
8. Gauss, C. F, Disquitiones Arithmeticae. Google Scholar
9. Kern-Isbrenner, G. and Rosenberger, G., A note on Numbers of the Form n — x2 + Nyl, Arch. Math.Google Scholar
10. Kulkarni, R., private communication. Google Scholar
11. Magnus, W., Karrass, A. and Solitar, D., Combinatorial Group Theory, Wiley Interscience, New York, 1966.Google Scholar
12. Newman, M., Integral Matrices, Academic Press, New York, 1972.Google Scholar
13. Sheingorn, M., private communication. Google Scholar
14. Williams, K., private communication. Google Scholar
15. Magnus, W, Non-Euclidean Tesselations and Their Groups, Academic Press, 1974.Google Scholar
16. Brenner, J. L. and Lyndon, R., Non-parabolic Subgroups of the Modular Group, J. Algebra (2) 77(1982), 311–322.Google Scholar