Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Milies, César Polcino
and
Juriaans, Stanley O.
2000.
Units of integral group rings of Frobenius groups.
Journal of Group Theory,
Vol. 3,
Issue. 3,
Juriaans, S. O.
De A. E Silva, A.
and
Souza Filho, A. C.
2015.
Traces of Torsion Units.
Communications in Algebra,
Vol. 43,
Issue. 9,
p.
3925.
Margolis, Leo
and
del Río, Ángel
2019.
Partial augmentations power property: A Zassenhaus Conjecture related problem.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 9,
p.
4089.


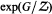 is finite,
is finite, 