No CrossRef data available.
Article contents
Toric degenerations of low-degree hypersurfaces
Part of:
Surfaces and higher-dimensional varieties
Computational aspects and applications
Special varieties
Published online by Cambridge University Press: 20 April 2023
Abstract
We show that a sufficiently general hypersurface of degree d in 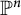 $\mathbb {P}^n$ admits a toric Gröbner degeneration after linear change of coordinates if and only if
$\mathbb {P}^n$ admits a toric Gröbner degeneration after linear change of coordinates if and only if 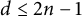 $d\leq 2n-1$.
$d\leq 2n-1$.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
N.I. was supported by an NSERC Discovery Grant. O.L. was supported by an NSERC undergraduate student research award.
References
Anderson, D.,
Okounkov bodies and toric degenerations
. Math. Ann. 356(2013), no. 3, 1183–1202.CrossRefGoogle Scholar
Bossinger, L., Lamboglia, S., Mincheva, K., and Mohammadi, F.,
Computing toric degenerations of flag varieties
. In: Smith, G. and Sturmfels, B. (eds.), Combinatorial algebraic geometry, vol. 80 of Fields Institute Communications, Fields Institute for Research in Mathematical Sciences, Toronto, ON, 2017, pp. 247–281.CrossRefGoogle Scholar
Coates, T., Corti, A., Galkin, S., Golyshev, V., and Kasprzyk, A.,
Mirror symmetry and Fano manifolds
. In: European Congress of Mathematics, European Mathematical Society, Zürich, 2013, pp. 285–300.Google Scholar
Harada, M. and Kaveh, K.,
Integrable systems, toric degenerations and Okounkov bodies
. Invent. Math. 202(2015), no. 3, 927–985.CrossRefGoogle Scholar
Ito, A.,
Seshadri constants via toric degenerations
. J. Reine Angew. Math. 695(2014), 151–174.CrossRefGoogle Scholar
Kaveh, K. and Manon, C.,
Khovanskii bases, higher rank valuations, and tropical geometry
. SIAM J. Appl. Algebra Geom. 3(2019), no. 2, 292–336.CrossRefGoogle Scholar
Kaveh, K., Manon, C., and Murata, T., Generic tropical initial ideals of Cohen–Macaulay algebras. J. Pure Appl. Algebra, 225(2021), no. 11, 106713. https://doi.org/10.1016/j.jpaa.2021.106713CrossRefGoogle Scholar
Kaveh, K., Manon, C., and Murata, T.,
On degenerations of projective varieties to complexity-one
 $T$
-varieties
. Int. Math. Res. Not. IMRN. 2023(2023), no. 3, 2665–2697.CrossRefGoogle Scholar
$T$
-varieties
. Int. Math. Res. Not. IMRN. 2023(2023), no. 3, 2665–2697.CrossRefGoogle Scholar
Maclagan, D. and Sturmfels, B., Introduction to tropical geometry, vol. 161, Graduate Studies in Mathematics, American Mathematical Society, Providence, RI, 2015.CrossRefGoogle Scholar



