Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:39:24.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological Properties of a Class of Higher-dimensional Self-affine Tiles

Part of: Discrete geometry Classical measure theory Designs and configurations Real and complex geometry

Published online by Cambridge University Press:  03 May 2019

Guotai Deng ,
Chuntai Liu  and
Sze-Man Ngai
Guotai Deng
Affiliation:
School of Mathematics and Statistics & Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan 430079, P. R. China Email: [email protected]
Chuntai Liu
Affiliation:
School of Mathematics and Computer Science, Wuhan Polytechnic University, Wuhan 430023, P. R. China Email: [email protected]
Sze-Man Ngai
Affiliation:
Key Laboratory of High Performance Computing and Stochastic Information Processing (HPCSIP) (Ministry of Education of China), College of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan 410081, P. R. China Department of Mathematical Sciences, Georgia Southern University, Statesboro, GA 30460-8093, USA Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a family of self-affine tiles in 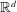$\mathbb{R}^{d}$ (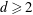$d\geqslant 2$) with noncollinear digit sets, which naturally generalizes a class studied originally by Q.-R. Deng and K.-S. Lau in 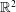$\mathbb{R}^{2}$, and its extension to 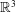$\mathbb{R}^{3}$ by the authors. We obtain necessary and sufficient conditions for the tiles to be connected and for their interiors to be contractible.

Keywords

self-affine tileconnectednessball-like tile

MSC classification

Primary: 28A80: Fractals
Secondary: 52C22: Tilings in $n$ dimensions 05B45: Tessellation and tiling problems 51M20: Polyhedra and polytopes; regular figures, division of spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 727 - 740
Copyright
© Canadian Mathematical Society 2019 

Footnotes

Author G. T. D. was supported by the Fundamental Research Funds for the Central Universities CCNU19TS071. Author C. T. L. was supported in part by the National Natural Science Foundation of China grant 11601403, China Scholarship Council and Research and Innovation Initiatives of WHPU 2018Y18. Author S. M. N. was supported in part by the National Natural Science Foundation of China grants 11771136 and 11271122, the Hunan Province Hundred Talents Program, Construct Program of the Key Discipline in Hunan Province, and a Faculty Research Scholarly Pursuit Funding from Georgia Southern University.

References

Akiyama, S. and Gjini, N., On the connectedness of self-affine attractors . Arch. Math. (Basel) 82(2004), 153–163. https://doi.org/10.1007/s00013-003-4820-z Google Scholar
Bandt, C. and Wang, Y., Disk-like self-affine tiles in ℝ2 . Discrete Comput. Geom. 26(2001), 591–601. https://doi.org/10.1007/s00454-001-0034-y Google Scholar
Conner, G. R. and Thuswaldner, J. M., Self-affine manifolds . Adv. Math. 289(2016), 725–783. https://doi.org/10.1016/j.aim.2015.11.022 Google Scholar
Deng, G., Liu, C., and Ngai, S.-M., Topological properties of a class of self-affine tiles in ℝ3 . Trans. Amer. Math. Soc. 370(2018), 1321–1350. https://doi.org/10.1090/tran/7055 Google Scholar
Deng, Q.-R. and Lau, K.-S., Connectedness of a class planar self-affine tiles . J. Math. Anal. Appl. 380(2011), 492–500. https://doi.org/10.1016/j.jmaa.2011.03.043 Google Scholar
Hata, M., On the structure of self-similar sets . Japan J. Appl. Math. 2(1985), 381–414. https://doi.org/10.1007/BF03167083 Google Scholar
He, X.-G., Kirat, I., and Lau, K.-S., Height reducing property of polynomials and self-affine tiles . Geom. Dedicata 152(2011), 153–164. https://doi.org/10.1007/s10711-010-9550-3 Google Scholar
Hutchinson, J. E., Fractals and self-similarity . Indiana Univ. Math. J. 30(1981), 713–747. https://doi.org/10.1512/iumj.1981.30.30055 Google Scholar
Kamae, T., Luo, J., and Tan, B., A gluing lemma for iterated function systems . Fractals 23(2015), 1550019, 10 pp. https://doi.org/10.1142/S0218348X1550019X Google Scholar
Kirat, I. and Lau, K.-S., On the connectedness of self-affine tiles . J. London Math. Soc. (2) 62(2000), 291–304. https://doi.org/10.1112/S002461070000106X Google Scholar
Kirat, I., Lau, K.-S., and Rao, H., Expanding polynomials and connectedness of self-affine tiles . Discrete Comput. Geom. 31(2004), 275–286. https://doi.org/10.1007/s00454-003-2879-8 Google Scholar
Lagarias, J. C. and Wang, Y., Self-affine tiles in ℝ n . Adv. Math. 121(1996), 21–49. https://doi.org/10.1006/aima.1996.0045 Google Scholar
Leung, K.-S. and Lau, K.-S., Disklikeness of planar self-affine tiles . Trans. Amer. Math. Soc. 359(2007), 3337–3355. https://doi.org/10.1090/S0002-9947-07-04106-2 Google Scholar
Leung, K. S. and Luo, J. J., Connectedness of planar self-affine sets associated with non-consecutive collinear digit sets . J. Math. Anal. Appl. 395(2012), 208–217. https://doi.org/10.1016/j.jmaa.2012.05.034 Google Scholar
Liu, J., Ngai, S.-M., and Tao, J., Connectedness of a class of two-dimensional self-affine tiles associated with triangular matrices . J. Math. Anal. Appl. 435(2016), 1499–1513. https://doi.org/10.1016/j.jmaa.2015.10.081 Google Scholar
Luo, J., Rao, H., and Tan, B., Topological structure of self-similar sets . Fractals 10(2002), 223–227. https://doi.org/10.1142/S0218348X0200104X Google Scholar
Ma, Y., Dong, X.-H., and Deng, Q.-R., The connectedness of some two-dimensional self-affine sets . J. Math. Anal. Appl. 420(2014), 1604–1616. https://doi.org/10.1016/j.jmaa.2014.06.054 Google Scholar