Published online by Cambridge University Press: 18 December 2020
A tight frame is the orthogonal projection of some orthonormal basis of 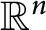 $\mathbb {R}^n$
onto
$\mathbb {R}^n$
onto 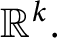 $\mathbb {R}^k.$
We show that a set of vectors is a tight frame if and only if the set of all cross products of these vectors is a tight frame. We reformulate a range of problems on the volume of projections (or sections) of regular polytopes in terms of tight frames and write a first-order necessary condition for local extrema of these problems. As applications, we prove new results for the problem of maximization of the volume of zonotopes.
$\mathbb {R}^k.$
We show that a set of vectors is a tight frame if and only if the set of all cross products of these vectors is a tight frame. We reformulate a range of problems on the volume of projections (or sections) of regular polytopes in terms of tight frames and write a first-order necessary condition for local extrema of these problems. As applications, we prove new results for the problem of maximization of the volume of zonotopes.
The author was supported by the Swiss National Science Foundation grant 200021_179133. The author acknowledges the financial support from the Ministry of Education and Science of the Russian Federation in the framework of MegaGrant no. 075-15-2019-1926.