No CrossRef data available.
Article contents
Terms of Lucas sequences having a large smooth divisor
Part of:
Sequences and sets
Published online by Cambridge University Press: 25 March 2022
Abstract
We show that the
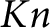 $Kn$
–smooth part of
$Kn$
–smooth part of
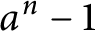 $a^n-1$
for an integer
$a^n-1$
for an integer
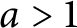 $a>1$
is
$a>1$
is
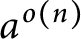 $a^{o(n)}$
for most positive integers n.
$a^{o(n)}$
for most positive integers n.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Bostan, A. and Mori, R.,
A simple and fast algorithm for computing the
 $N$
-th term of a linearly recurrent sequence
. SOSA 2021, 118–132.Google Scholar
$N$
-th term of a linearly recurrent sequence
. SOSA 2021, 118–132.Google Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers. Sixth edition. Revised by Heath-Brown, D. R. and Silverman, J. H.. With a foreword by Andrew Wiles. Oxford University Press, Oxford, 2008. xxii+621 pp.Google Scholar
Murty, R. and Wong, S.,
The ABC conjecture and prime divisors of the Lucas and Lehmer sequences
. In Number theory for the millennium, III (Urbana, IL, 2000), A K Peters, Natick, MA, 2002, pp. 43–54.Google Scholar
Shamir, A.,
Factoring numbers in O(logn) arithmetic steps
. Inf. Process. Lett. 8(1979), no. 1, 28–31.Google Scholar
Shparlinski, I. E.,
Some arithmetic properties of recurrence sequences
. Math. Zam. 47(1990), 124–131; Translation in Math. Notes 47 (1990), 612–617.Google Scholar
Stewart, C. L.,
On divisors of Lucas and Lehmer numbers
. Acta Math. 211(2013), 291–314.Google Scholar



