Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-15T18:52:58.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Tensor Products of Banach Algebras*

Published online by Cambridge University Press:  20 November 2018

Boaz Natzitz
Boaz Natzitz*
Affiliation:
McGill University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [3] Gelbaum defined the tensor product A ⊗CB of three commutative Banach algebras, A, B and C and established some of its properties. Various examples are given and the particular case where A, B and C are group algebras of L.C.A. groups G, H and K respectively, is discussed there. It is shown there that if K is compact L1(G) ⊗ L1(K) L1(H) is isomorphic to 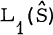where 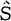is L.C.A. 1 L (K) 1 1 if and only if L1(G) ⊗ L1(K) L1(H) is semisimple.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 5 , December 1968 , pp. 691 - 701
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

**

The author wishes to thank Professor B.R. Gelbaum for his advice and encouragement.

*

Supported by Air Force Grant AFOSR-407-63, Yale University and N.S.F. Grant G. 24295, University of Minnesota.

References

1. Cohen, P.J., Factorization in group algebras. Duke Math. J. 26 (1959) 199-205.Google Scholar
2. Gelbaum, B.R., Tensor products and related questions. Trans. Amer. Math. Soc. 103 (1962) 525-547.Google Scholar
3. Gelbaum, B.R., Tensor products over Banach algebras. Trans. Amer. Math. Soc. 118 (1965) 131-149.Google Scholar
4. Grothendieck, A., Produits tensoriels topologiques et espaces nucleaires. Mem. Amer. Math. Soc. 16 (1955).Google Scholar
5. Hewitt, E., The range of certain convolution operators. Math. Scand. 15 (1964) 147-155.Google Scholar
6. Hewitt, E. and Ross, K., Abstract harmonic analysis I (Springer, Berlin-Gottingen-Heidelberg, 1963).Google Scholar
7. Loomis, L. H., An introduction to abstract harmonic analysis. (Van Nostrand, New York, 1953).Google Scholar
8. Rudin, W., Fourier analysis on groups. (Interscience, New York 1962).Google Scholar
9. Schaefer, H., Topological vector spaces. (Macmillan, New York 1966).Google Scholar
10. Schwartz, L., Produits tensoriels topologiques d'espaces vectoriels topologiques. Fac. Sci. de Paris, Seminaire Schwartz (1953-1954).Google Scholar
11. Tomiyama, J., Tensor products of commutative Banach algebras Tohoku, Math. J. 12 (1960) 147-154.Google Scholar
12. Weil, A., L'integration sans les groupes topologiques et ses application. (Hermann, Paris 1953).Google Scholar