Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T01:39:51.683Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetries of Kirchberg Algebras

Published online by Cambridge University Press:  20 November 2018

David J. Benson ,
Alex Kumjian  and
N. Christopher Phillips
David J. Benson
Affiliation:
Department of Mathematics University of Georgia Athens, GA 30602-7403 USA, email: [email protected]
Alex Kumjian
Affiliation:
Department of Mathematics University of Nevada Reno, NV 89557-0045 USA, email: [email protected]
N. Christopher Phillips
Affiliation:
Department of Mathematics University of Oregon Eugene, OR 97403-1222 USA, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 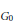${{G}_{0}}$ and 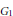${{G}_{1}}$ be countable abelian groups. Let 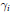${{\gamma }_{i}}$ be an automorphism of 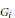${{G}_{i}}$ of order two. Then there exists a unital Kirchberg algebra 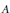$A$ satisfying the Universal Coefficient Theorem and with 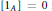$[{{1}_{A}}]\,=\,0$ in 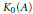${{K}_{0}}(A)$, and an automorphism 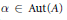$\alpha \,\in \,\text{Aut}(A)$ of order two, such that 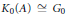${{K}_{0}}(A)\,\cong \,{{G}_{0}}$, such that 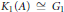${{K}_{1}}(A)\,\cong \,{{G}_{1}}$, and such that 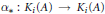${{\alpha }_{*}}\,:\,{{K}_{i}}(A)\,\to \,{{K}_{i}}(A)$ is 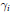${{\gamma }_{i}}$. As a consequence, we prove that every 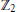${{\mathbb{Z}}_{2}}$-graded countable module over the representation ring 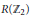$R({{\mathbb{Z}}_{2}})$ of 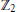${{\mathbb{Z}}_{2}}$ is isomorphic to the equivariant 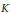$K$-theory 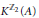${{K}^{{{\mathbb{Z}}_{2}}}}(A)$ for some action of 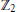${{\mathbb{Z}}_{2}}$ on a unital Kirchberg algebr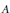a $A$.

Along the way, we prove that every not necessarily finitely generated 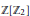$\mathbb{Z}\left[ {{\mathbb{Z}}_{2}} \right]$-module which is free as a 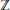$\mathbb{Z}$-module has a direct sum decomposition with only three kinds of summands, namely 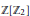$\mathbb{Z}\left[ {{\mathbb{Z}}_{2}} \right]$ itself and 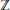$\mathbb{Z}$ on which the nontrivial element of 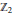${{\mathbb{Z}}_{2}}$ acts either trivially or by multiplication by −1.

Keywords

20C1046L5519K9919L4746L4046L80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 509 - 528
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bass, H., Big projective modules are free. Illinois J. Math. 7 (1963), 24–31.Google Scholar
[2] Benson, D. J. and Goodearl, K. R., Periodic flat modules, and flat modules for finite groups. Pacific J. Math. 196 (2000), 45–67.Google Scholar
[3] Blackadar, B., K-Theory for Operator Algebras. MSRI Publication Series 5, Springer-Verlag, New York-Heidelberg-Berlin-Tokyo, 1986.Google Scholar
[4] Butler, M. C. R., Campbell, J. M. and Kovács, L. G., Infinite rank integral representations of groups and orders of finite lattice type. In preparation.Google Scholar
[5] Butler, M. C. R. and Kovács, L. G., Large lattices over classical orders of finite lattice type. Draft preprint.Google Scholar
[6] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
[7] Cuntz, J., K-theory for certain C*-algebras. Ann. Math. 113 (1981), 181–197.Google Scholar
[8] Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras. Interscience Publishers, New York-London-Sydney, 1962.Google Scholar
[9] Elliott, G. A. and Rørdam, M., Classification of certain infinite simple C*-algebras II. Comment. Math. Helv. 70 (1995), 615–638.Google Scholar
[10] Fuchs, L., Infinite Abelian Groups, Vol. I. Academic Press, New York-London, 1970.Google Scholar
[11] Hua, L. K. and Reiner, I., Automorphisms of the unimodular group. Trans. Amer.Math. Soc. 71 (1951), 331–348.Google Scholar
[12] Jeong, J. A. and Osaka, H., Extremally rich C*-crossed products and the cancellation property. J. Austral. Math. Soc. (Ser. A) 64 (1998), 285–301.Google Scholar
[13] Kirchberg, E., Commutants of unitaries in UHF algebras and functorial properties of exactness. J. Reine Angew.Math. 452 (1994), 39–77.Google Scholar
[14] Kirchberg, E., The classification of purely infinite C*-algebras using Kasparov's theory. Preliminary preprint (3rd draft).Google Scholar
[15] Kumjian, A., On certain Cuntz-Pimsner algebras. Preprint.Google Scholar
[16] Mac Lane, S., Categories for the Working Mathematician. Graduate Texts in Math. 5, Springer-Verlag, New York-Heidelberg-Berlin, 1971.Google Scholar
[17] Pedersen, G. K.,C*-Algebras and their Automorphism Groups. Academic Press, London-New York-San Francisco, 1979.Google Scholar
[18] Phillips, N. C., Equivariant K-Theory and Freeness of Group Actions on C*-Algebras. Lecture Notes in Math. 1274, Springer-Verlag, Berlin-Heidelberg-New York-London-Paris-Tokyo, 1987.Google Scholar
[19] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5 (2000), 49–114 (electronic).Google Scholar
[20] Pimsner, M., A class of C*-algebras generalizing both Cuntz-Krieger algebras and crossed products by Z. In: Free Probability Theory (Waterloo, ON, 1995), Fields Inst. Commun. 12, Amer.Math. Soc., Providence, RI, 1997, 189–212.Google Scholar
[21] Rieffel, M. A., Actions of finite groups on C*-algebras. Math. Scand. 47 (1980), 157–176.Google Scholar
[22] Rørdam, M. and Størmer, E., Classification of nuclear C*-algebras. Entropy in operator algebras. Springer-Verlag, Berlin, 2002.Google Scholar
[23] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55 (1987), 431–474.Google Scholar
[24] Schochet, C., Topological methods for C*-algebras II: geometric resolutions and the Künneth formula. Pacific J. Math. 98 (1982), 443–458.Google Scholar
[25] Schochet, C., Topological methods for C*-algebras III: axiomatic homology. Pacific J. Math. 114 (1984), 399–445.Google Scholar
[26] Swan, R. G., Induced representations and projective modules. Ann. of Math. 71 (1960), 552–578.Google Scholar
[27] Takai, H., On a duality for crossed products of C*-algebras. J. Funct. Anal. 19 (1975), 25–39.Google Scholar