Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-09T19:59:01.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur les algèbres de Lie associées à une connexion

Published online by Cambridge University Press:  20 November 2018

Princy Randriambololondrantomalala ,
H. S. G. Ravelonirina  and
F. M. Anona
Princy Randriambololondrantomalala
Affiliation:
Département de Mathématiques et Informatique, Faculté des Sciences, Université d’Antananarivo, BP 906, Ambohitsaina 101-Antananarivo, Madagascar courriell: [email protected]@[email protected]
H. S. G. Ravelonirina
Affiliation:
Département de Mathématiques et Informatique, Faculté des Sciences, Université d’Antananarivo, BP 906, Ambohitsaina 101-Antananarivo, Madagascar courriell: [email protected]@[email protected]
F. M. Anona
Affiliation:
Département de Mathématiques et Informatique, Faculté des Sciences, Université d’Antananarivo, BP 906, Ambohitsaina 101-Antananarivo, Madagascar courriell: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\Gamma$ be a connection on a smooth manifold 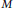$M$. In this paper we give some properties of $\Gamma$ by studying the corresponding Lie algebras. In particular, we compute the first Chevalley–Eilenberg cohomology space of the horizontal vector fields Lie algebra on the tangent bundle of 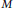$M$, whose the corresponding Lie derivative of $\Gamma$ is null, and of the horizontal nullity curvature space.

Résumé

Résumé

Etant donné une connexion Γ sur une variété différentiable 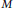$M$, dans ce papier on se propose de donner quelques propriétés de $\Gamma$ en étudiant les algèbres de Lie associées à cette connexion. En particulier, on calcule le premier espace de cohomologie de Chevalley–Eilenberg de la partie horizontale de l’algèbre de Lie des champs de vecteurs sur le fibré tangent de 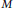$M$ dont la dérivée de Lie correspondante de $\Gamma$ est nulle, et de l’espace de nullité horizontal de la courbure.

Keywords

17B6653B1517B56algèbre de Lieconnexioncohomologie de Chevalley–Eilenbergchamps dont la dérivée de Lie correspondante à une connexion est nulleespace de nullité de la courbure
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 692 - 703
Copyright
Copyright © Canadian Mathematical Society 2015

References

Références

[1] Anona, M., P. Randriambololondrantomalala et H. S. G. Ravelonirina, Sur les algèbres de Lie des champs de vecteurs polynomiaux. Afr. Diaspora J. Math. 10(2010), 87–95.Google Scholar
[2] Anona, M., P. Randriambololondrantomalala et H. S. G. Ravelonirina, Sur les algèbres de Lie d'une distribution et d'un feuilletage généralisé. Afr. Diaspora J. Math. 10(2010), 135–144.Google Scholar
[3] Anona, M., P. Randriambololondrantomalala et H. S. G. Ravelonirina, Sur les algèbres de Lie d'un système de champs de vecteurs permutables. Ital. J. Pure Appl. Math. 29(2012), 163–174.Google Scholar
[4] Bourbaki, N., Groupes et algèbres de Lie. Hermann, Paris, 1960.Google Scholar
[5] Grifone, J., Structure presque-tangente et connexions I. Ann. Inst. Fourier Grenoble 22(1972), 287–334. http://dx.doi.Org/10.58O2/aif.4O7 Google Scholar
[6] Klein, J., On Lie Algebras of vector fields defined by vector forms. Colloq. Math. Soc. Jânos Bolyai 46, North-Holland, Amsterdam, 1988.Google Scholar
[7] Nakanishi, N., The first cohomology groups of infinite dimensional Lie algebras. Pub. RIMS. Kyoto Univ. 18(1982), 1–16. http://dx.doi.Org/10.2977/prims/1195184013 Google Scholar
[8] Youssef, N. L., Sur les tenseurs de courbure de la connexion de Berwald et ses distributions de nullité. Tensor N.S. 36(1982), 275–280.Google Scholar
[9] Weibel, C., An introduction to homological algebra. Cambridge Stud. Adv. Math. 38, Cambridge University Press, Cambridge, 1994.Google Scholar