Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T19:56:43.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Sumsets of semiconvex sets

Part of: Sequences and sets Designs and configurations

Published online by Cambridge University Press:  26 February 2021

Imre Ruzsa  and
Jozsef Solymosi
Imre Ruzsa*
Affiliation:
Alfréd Rényi Institute of Mathematics, Budapest, Hungary
Jozsef Solymosi
Affiliation:
University of British Columbia, Department of Mathematics, Vancouver, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate additive properties of sets 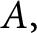$A,$ where 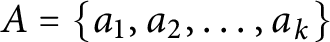$A=\{a_1,a_2,\ldots ,a_k\}$ is a monotone increasing set of real numbers, and the differences of consecutive elements are all distinct. It is known that 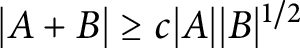$|A+B|\geq c|A||B|^{1/2}$ for any finite set of numbers 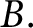$B.$ The bound is tight up to the constant multiplier. We give a new proof to this result using bounds on crossing numbers of geometric graphs. We construct examples showing the limits of possible improvements. In particular, we show that there are arbitrarily large sets with different consecutive differences and sub-quadratic sumset size.

Keywords

sumset inequalitiesconvex sets of numbersadditive combinatorics

MSC classification

Primary: 05B10: Difference sets (number-theoretic, group-theoretic, etc.)
Secondary: 11B13: Additive bases, including sumsets 11B05: Density, gaps, topology
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 84 - 94
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M., Chvátal, V., Newborn, M., and Szemerédi, E., Crossing-free subgraphs . Ann. Discrete Math. 12(1982), 9–12.Google Scholar
Elekes, G., Nathanson, M. B., and Ruzsa, I. Z., Convexity and sumsets . J. Number Theory 83(2000), no. 2, 194–201.10.1006/jnth.1999.2386CrossRefGoogle Scholar
Hanson, B., Roche–Newton, O., and Rudnev, M., Higher convexity and iterated sum sets. To appear in Combinatorica, 2020. arXiv:2005.00125[math.NT] 10.1007/s00493-021-4578-6CrossRefGoogle Scholar
Hegyvári, N., On consecutive sums in sequences . Acta Math. Hungar. 48(1986), nos. 1–2, 193–200.CrossRefGoogle Scholar
Li, L. and Roche-Newton, O., Convexity and a sum-product type estimate . Acta Arith. 156(2012), 247–255.10.4064/aa156-3-3CrossRefGoogle Scholar
Pach, J., Solymosi, J., and Tardos, G., Crossing numbers of imbalanced graphs . J. Graph Theory 64(2010), no. 1, 12–21.10.1002/jgt.20435CrossRefGoogle Scholar
Rudnev, M. and Stevens, S., An update on the sum-product problem . Preprint, 2020. arXiv:2005.11145 10.1017/S0305004121000633CrossRefGoogle Scholar
Ruzsa, I., Shakan, G., Solymosi, J., and Szemerédi, E., Distinct consecutive differences. In: Springer volume: Combinatorial and additive number theory IV. Preprint, 2021. arXiv:1910.02159[math.CO]CrossRefGoogle Scholar
Schoen, T., On convolutions of convex sets and related problems . Canad. Math. Bull. 57(2014), no. 4, 877–883.10.4153/CMB-2013-041-8CrossRefGoogle Scholar
Schoen, T. and Shkredov, I., On sumsets of convex sets . Combin. Probab. Comput. 20(2011), no. 5, 793–798.CrossRefGoogle Scholar
Shahrokhi, F., Sýkora, O., Székely, L. A., and Vrt’o, I., Bounds for convex crossing numbers . In: Computing and combinatorics, Lecture Notes in Computer Science, 2697, Springer, Berlin, 2003, pp. 487–495.Google Scholar
Shkredov, I., On sums of Szemerédi–Trotter sets . Proc. Steklov Inst. Math. 289(2015), 300–309.10.1134/S0081543815040185CrossRefGoogle Scholar
Shkredov, I., Personal communication (2020 August).Google Scholar
Stevens, S. and Warren, A., On sum sets of convex functions . Preprint, 2021. arXiv:2102.05446[math.CO]Google Scholar
Székely, L., Crossing numbers and hard Erdős problems in discrete geometry . Combin. Probab. Comput. 6(1997), no. 3, 353–358.10.1017/S0963548397002976CrossRefGoogle Scholar