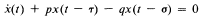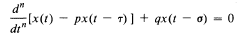Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zafer, A.
and
Dahiya, R.S.
1993.
Oscillation of bounded solutions of neutral differential equations.
Applied Mathematics Letters,
Vol. 6,
Issue. 2,
p.
43.
Erbe, L.
and
Kong, Qingkai
1994.
Explicit conditions for oscillation of neutral differential systems.
Hiroshima Mathematical Journal,
Vol. 24,
Issue. 2,
Zhang, B.G.
Yu, J.S.
and
Wang, Z.C.
1995.
Oscillations of Higher Order Neutral Differential Equations.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 1,
Derfel, Gregory
1995.
Operator Theory and Boundary Eigenvalue Problems.
p.
100.
Dahiya, R. S.
2001.
Differential Equations and Nonlinear Mechanics.
p.
75.
Zhang, B.G.
and
Ren, Hongshan
2003.
Necessary and sufficient conditions for the oscillation of certain delay differential equations.
Applied Mathematics Letters,
Vol. 16,
Issue. 3,
p.
409.
2004.
Nonoscillation and Oscillation Theory for Functional Differential Equations.
p.
359.
Lay-Ekuakille, Aimé
and
Trotta, Amerigo
2011.
Predicting VOC Concentration Measurements: Cognitive Approach for Sensor Networks.
IEEE Sensors Journal,
Vol. 11,
Issue. 11,
p.
3023.