Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Metaftsis, V
and
Raptis, E
2001.
Subgroup Separability of HNN-Extensions with Abelian Base Group.
Journal of Algebra,
Vol. 245,
Issue. 1,
p.
42.
Kim, Goansu
and
Tang, C.Y.
2002.
Separability Properties of Certain Tree Products of Groups.
Journal of Algebra,
Vol. 251,
Issue. 1,
p.
323.
Tang, C
and
Kim, Goansu
2008.
Applications of Group Theory to Combinatorics.
p.
59.
Zhou, Wei
and
Kim, Goansu
2017.
Abelian subgroup separability of certain generalized free products of free or finitely generated nilpotent groups.
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 1,
p.
222.
Ribes, Luis
2017.
Profinite Graphs and Groups.
Vol. 66,
Issue. ,
p.
391.


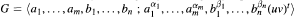 where t ≥ 1 and
where t ≥ 1 and 