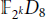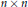Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
GILDEA, JOE
2011.
UNITS OF THE GROUP ALGEBRA 𝔽2κ(C2× D8).
Journal of Algebra and Its Applications,
Vol. 10,
Issue. 04,
p.
643.
Gildea, Joe
2011.
The structure of the unit group of the group algebra $\mathbb{F}_{2^k } A_4 $.
Czechoslovak Mathematical Journal,
Vol. 61,
Issue. 2,
p.
531.
Gildea, Joe
2012.
Units of Group Algebras of Non-Abelian Groups of Order 16 and Exponent 4 over $${\mathbb{F}_{2^k}}$$.
Results in Mathematics,
Vol. 61,
Issue. 3-4,
p.
245.
RAZA, ZAHID
and
AHMAD, MAQSOOD
2013.
ON THE UNITARY UNITS OF THE GROUP ALGEBRA 𝔽2mM16.
Journal of Algebra and Its Applications,
Vol. 12,
Issue. 08,
p.
1350059.
RAZA, ZAHID
and
AHMAD, MAQSOOD
2014.
ON THE STRUCTURE OF THE UNITARY SUBGROUP OF THE GROUP ALGEBRA 𝔽2qD2n.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 04,
p.
1350139.
Makhijani, Neha
Sharma, R. K.
and
Srivastava, J. B.
2014.
The unit group of finite group algebra of a generalized dihedral group.
Asian-European Journal of Mathematics,
Vol. 07,
Issue. 02,
p.
1450034.
KAUR, KULDEEP
and
KHAN, MANJU
2014.
UNITS IN F2D2p.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 02,
p.
1350090.
Tang, Gaohua
Wei, Yangjiang
and
Li, Yuanlin
2014.
Unit groups of group algebras of some small groups.
Czechoslovak Mathematical Journal,
Vol. 64,
Issue. 1,
p.
149.
Raza, Zahid
and
Ali, Riasat
2015.
On the unitary units of the group algebra 𝔽2kQ16.
Asian-European Journal of Mathematics,
Vol. 08,
Issue. 01,
p.
1550013.
Makhijani, Neha
Sharma, R. K.
and
Srivastava, J. B.
2016.
A note on the structure of $$\mathbb{F}_{p^k}A_5/J (\mathbb{F}_{p^k}A_5)$$.
Acta Scientiarum Mathematicarum,
Vol. 82,
Issue. 1-2,
p.
29.
Makhijani, Neha
Sharma, R.K.
and
Srivastava, J.B.
2016.
Units in finite dihedral and quaternion group algebras.
Journal of the Egyptian Mathematical Society,
Vol. 24,
Issue. 1,
p.
5.
Makhijani, Neha
Sharma, R.K.
and
Srivastava, J.B.
2016.
The unit group of some special semi-simple group algebras.
Quaestiones Mathematicae,
Vol. 39,
Issue. 1,
p.
9.
Raza, Zahid
and
Ahmad, Maqsood
2018.
Structure of the unitary subgroup of the group algebra 𝔽2n(QD)16.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 04,
p.
1850060.
Laver, V.
and
Balogh, Zs.
2020.
Унiтарнi пiдгрупи комутативних групових алгебр характеристики 2*.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 72,
Issue. 6,
p.
751.
Balogh, Z.
and
Laver, V.
2020.
Unitary Subgroups of Commutative Group Algebras of the Characteristic Two.
Ukrainian Mathematical Journal,
Vol. 72,
Issue. 6,
p.
871.
BALOGH, Zsolt Adam
2021.
ON UNITARY SUBGROUPS OF GROUP ALGEBRAS.
International Electronic Journal of Algebra,
Vol. 29,
Issue. 29,
p.
187.
Rajpurohit, Gourishankar
Sharma, Mahesh Kumar
Sharma, Gyanprakash
and
Anita, Anita
2021.
ROLE OF PANCHKARMA THERAPY IN MANAGEMENT OF DARUNAKA (SEBORRHOEIC DERMATITIS) - A SINGLE CASE STUDY.
International Ayurvedic Medical Journal,
Vol. 9,
Issue. 11,
p.
2880.
SAHAI, Meena
and
ANSARI, Sheere Farhat
2021.
THE GROUP OF UNITS OF GROUP ALGEBRAS OF GROUPS $D_{30}$ AND $C_3 \times D_{10}$ OVER A FINITE FIELD OF CHARACTERISTIC $3$.
International Electronic Journal of Algebra,
Vol. 29,
Issue. 29,
p.
165.
Creedon, Leo
Hughes, Kieran
and
Szabo, Steve
2021.
A comparison of group algebras of dihedral and quaternion groups.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 32,
Issue. 3,
p.
245.
BALOGH, Zsolt Adam
2022.
On the isomorphism of unitary subgroups of noncommutative group algebras.
Journal of Algebra Combinatorics Discrete Structures and Applications,
Vol. 9,
Issue. 2,
p.
45.