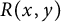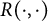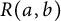1 Introduction
Given a finite digraph
![]() $\Gamma $
with vertex set
$\Gamma $
with vertex set
![]() $V(\Gamma )$
and arc set
$V(\Gamma )$
and arc set
![]() $A(\Gamma )$
(without loops or parallel arcs) and an element
$A(\Gamma )$
(without loops or parallel arcs) and an element
![]() $R(a,b)$
in the free group of rank 2 generated by a and b, the digraph group
$R(a,b)$
in the free group of rank 2 generated by a and b, the digraph group
![]() $G_{\Gamma} (R)$
is the group defined by the presentation
$G_{\Gamma} (R)$
is the group defined by the presentation
These groups were introduced in [Reference Cuno and Williams7] and contain the graph groups or right angled Artin groups as special cases (by setting
![]() $R(a,b)=aba^{-1}b^{-1}$
). Formal definitions of undefined terms of the introduction are given in Section 2.
$R(a,b)=aba^{-1}b^{-1}$
). Formal definitions of undefined terms of the introduction are given in Section 2.
Digraph groups with balanced presentations (i.e., digraph groups corresponding to digraphs with an equal number of vertices and arcs) were considered in [Reference Cuno and Williams7] and digraph groups corresponding to digraphs with one more arc than vertices were considered in [Reference Cihan5]. Two families of finite, noncyclic, digraph groups were obtained in [Reference Cihan and Williams6, Corollaries A2 and B2]. In this article, we consider digraph groups
![]() $G_{\Gamma} (R)$
where
$G_{\Gamma} (R)$
where
![]() $\Gamma $
is a strong digraph that is digon-free and triangle-free. We state our results in terms of the period of the digraph (that is, the greatest common divisor of the lengths of its cycles), the one-relator group
$\Gamma $
is a strong digraph that is digon-free and triangle-free. We state our results in terms of the period of the digraph (that is, the greatest common divisor of the lengths of its cycles), the one-relator group
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
, and integers
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
, and integers
![]() $\alpha ,\beta $
, which denote the exponent sums of a and of
$\alpha ,\beta $
, which denote the exponent sums of a and of
![]() $b^{-1}$
in
$b^{-1}$
in
![]() $R(a,b)$
, respectively.
$R(a,b)$
, respectively.
In this context, [Reference Pride17, Theorem 3] concerns digraph groups
![]() $G_{\Gamma} (R)$
where
$G_{\Gamma} (R)$
where
![]() $\Gamma $
is a cycle of length at least 4, and can be expressed as follows:
$\Gamma $
is a cycle of length at least 4, and can be expressed as follows:
Theorem 1.1 [Reference Pride17]
Let
![]() $\Gamma $
be a cycle of length
$\Gamma $
be a cycle of length
![]() $n\geq 4$
and let
$n\geq 4$
and let
![]() $R(a, b)$
be a cyclically reduced word that involves both a and b with exponent sums
$R(a, b)$
be a cyclically reduced word that involves both a and b with exponent sums
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in a and
$\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() $G_{\Gamma} (R)$
is finite if and only if
$G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\beta \neq 0$
,
$\beta \neq 0$
,
![]() ${\mathrm {gcd}\{\alpha ,\beta \}=1}$
,
${\mathrm {gcd}\{\alpha ,\beta \}=1}$
,
![]() $\alpha ^n\neq \beta ^n$
,
$\alpha ^n\neq \beta ^n$
,
![]() $a^\alpha =b^\beta $
in K, in which case
$a^\alpha =b^\beta $
in K, in which case
![]() $G_{\Gamma} (R)$
is cyclic of order
$G_{\Gamma} (R)$
is cyclic of order
![]() $|\alpha ^n-\beta ^n|$
.
$|\alpha ^n-\beta ^n|$
.
When
![]() $\Gamma $
is a cycle, the digraph group
$\Gamma $
is a cycle, the digraph group
![]() $G_{\Gamma} (R)$
is an example of a cyclically presented group [Reference Johnson12, Chapter III, Section 9]. As observed in [Reference Pride17], Theorem 1.1 cannot be directly extended to the cases
$G_{\Gamma} (R)$
is an example of a cyclically presented group [Reference Johnson12, Chapter III, Section 9]. As observed in [Reference Pride17], Theorem 1.1 cannot be directly extended to the cases
![]() $n=2$
and
$n=2$
and
![]() $n=3$
, that is, to the cases where
$n=3$
, that is, to the cases where
![]() $\Gamma $
is neither digon-free nor triangle-free. Examples that demonstrate this include the Macdonald groups
$\Gamma $
is neither digon-free nor triangle-free. Examples that demonstrate this include the Macdonald groups
![]() $Mac(a,a)$
which, for
$Mac(a,a)$
which, for
![]() $a\in \mathbb {Z}$
,
$a\in \mathbb {Z}$
,
![]() $a\neq 0,1,2$
, are finite of rank 2 [Reference Macdonald13, Reference Ocampo and Szechtman16]; the Fox groups
$a\neq 0,1,2$
, are finite of rank 2 [Reference Macdonald13, Reference Ocampo and Szechtman16]; the Fox groups
![]() $\langle {x,y}\ |\ {xy^n=y^lx, yx^n=x^ly} \rangle $
which are finite of rank 2 if
$\langle {x,y}\ |\ {xy^n=y^lx, yx^n=x^ly} \rangle $
which are finite of rank 2 if
![]() $(n,l)=1$
,
$(n,l)=1$
,
![]() $n\neq l$
[Reference Campbell and Robertson4]; the Mennicke groups
$n\neq l$
[Reference Campbell and Robertson4]; the Mennicke groups
![]() $M(q,q,q)$
, which are finite of rank 3 for each
$M(q,q,q)$
, which are finite of rank 3 for each
![]() $q\geq 3$
[Reference Mennicke15]; and the Johnson groups
$q\geq 3$
[Reference Mennicke15]; and the Johnson groups
![]() $J(q,q,q)$
which are finite of rank 3 for each even
$J(q,q,q)$
which are finite of rank 3 for each even
![]() $q\geq 2$
[Reference Johnson11], [Reference Johnson12, p. 70]. A strong digraph is one in which there is a path joining every pair of vertices, and so the cycle of length n is a strong digraph of period n. In this article, we generalize Theorem 1.1 by replacing the cycle of length at least 4 by a nontrivial, strong digraph that is digon-free and triangle-free. Our main result is the following:
$q\geq 2$
[Reference Johnson11], [Reference Johnson12, p. 70]. A strong digraph is one in which there is a path joining every pair of vertices, and so the cycle of length n is a strong digraph of period n. In this article, we generalize Theorem 1.1 by replacing the cycle of length at least 4 by a nontrivial, strong digraph that is digon-free and triangle-free. Our main result is the following:
Theorem 1.2 Let
![]() $\Gamma $
be a nontrivial, strong digraph of period p that is digon-free and triangle-free and let
$\Gamma $
be a nontrivial, strong digraph of period p that is digon-free and triangle-free and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() $G_{\Gamma} (R)$
is finite if and only if
$G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\beta \neq 0$
,
$\beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
,
$\alpha ^p\neq \beta ^p$
,
![]() $a^\alpha =b^\beta $
in K, in which case
$a^\alpha =b^\beta $
in K, in which case
![]() $G_{\Gamma} (R)$
is cyclic of order
$G_{\Gamma} (R)$
is cyclic of order
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
In Section 5, we apply this to the Cayley digraph of the generalized quaternion group, to circulant digraphs, and to Cartesian and direct products of strong digraphs.
2 Preliminaries
A digraph (or directed graph)
![]() $\Gamma $
consists of a finite set
$\Gamma $
consists of a finite set
![]() $V(\Gamma )$
of vertices and a set
$V(\Gamma )$
of vertices and a set
![]() $A(\Gamma )$
of arcs, which are ordered pairs
$A(\Gamma )$
of arcs, which are ordered pairs
![]() $[u,v]$
of distinct vertices (as such,
$[u,v]$
of distinct vertices (as such,
![]() $\Gamma $
does not contain parallel arcs or loops); it is nontrivial if it has at least two vertices. The underlying graph of
$\Gamma $
does not contain parallel arcs or loops); it is nontrivial if it has at least two vertices. The underlying graph of
![]() $\Gamma $
is the graph with vertex set
$\Gamma $
is the graph with vertex set
![]() $V(\Gamma )$
and edge set
$V(\Gamma )$
and edge set
![]() $E(\Gamma )$
consisting of all unordered pairs
$E(\Gamma )$
consisting of all unordered pairs
![]() $\{u,v\}$
(edges), where
$\{u,v\}$
(edges), where
![]() $[u,v]\in A(\Gamma )$
. A digon is a subdigraph of
$[u,v]\in A(\Gamma )$
. A digon is a subdigraph of
![]() $\Gamma $
consisting of vertices
$\Gamma $
consisting of vertices
![]() $u,v\in V(\Gamma )$
and arcs
$u,v\in V(\Gamma )$
and arcs
![]() $[u,v],[v,u] \in A(\Gamma )$
. A triangle is a subdigraph of
$[u,v],[v,u] \in A(\Gamma )$
. A triangle is a subdigraph of
![]() $\Gamma $
consisting of vertices
$\Gamma $
consisting of vertices
![]() $u,v,w\in V(\Gamma )$
and either arcs
$u,v,w\in V(\Gamma )$
and either arcs
![]() $[u,v],[v,w],[w,u]\in A(\Gamma )$
or arcs
$[u,v],[v,w],[w,u]\in A(\Gamma )$
or arcs
![]() $[u,v],[v,w],[u,w]\in A(\Gamma )$
. A digraph is said to be digon-free (resp. triangle-free) if it contains no digons (resp. triangles). A tournament is a digraph
$[u,v],[v,w],[u,w]\in A(\Gamma )$
. A digraph is said to be digon-free (resp. triangle-free) if it contains no digons (resp. triangles). A tournament is a digraph
![]() $\Gamma $
in which exactly one of
$\Gamma $
in which exactly one of
![]() $[u,v],[v,u]\in A(\Gamma )$
for each pair of vertices
$[u,v],[v,u]\in A(\Gamma )$
for each pair of vertices
![]() $u,v\in V(\Gamma )$
. A walk (of length
$u,v\in V(\Gamma )$
. A walk (of length
![]() $n-1$
) in a digraph
$n-1$
) in a digraph
![]() $\Gamma $
is a collection of vertices
$\Gamma $
is a collection of vertices
![]() $v_1,v_2,\dots ,v_n$
such that
$v_1,v_2,\dots ,v_n$
such that
![]() $[v_i,v_{i+1}]\in A(\Gamma )$
for each
$[v_i,v_{i+1}]\in A(\Gamma )$
for each
![]() $1\leq i<n$
; it is closed if
$1\leq i<n$
; it is closed if
![]() $v_n=v_1$
. We denote such a walk
$v_n=v_1$
. We denote such a walk
![]() $v_1\rightarrow v_2 \rightarrow \cdots \rightarrow v_n$
. A path is a walk in which the vertices are distinct. A cycle (of length n) is a collection of distinct vertices
$v_1\rightarrow v_2 \rightarrow \cdots \rightarrow v_n$
. A path is a walk in which the vertices are distinct. A cycle (of length n) is a collection of distinct vertices
![]() $v_1,v_2,\dots ,v_n$
such that
$v_1,v_2,\dots ,v_n$
such that
![]() $[v_i,v_{i+1}]\in A(\Gamma )$
for each
$[v_i,v_{i+1}]\in A(\Gamma )$
for each
![]() $1\leq i<n$
and
$1\leq i<n$
and
![]() $[v_n,v_1]\in A(\Gamma )$
. The period
$[v_n,v_1]\in A(\Gamma )$
. The period
![]() $p(\Gamma )$
of a digraph
$p(\Gamma )$
of a digraph
![]() $\Gamma $
is the greatest common divisor of the lengths of its cycles, and so
$\Gamma $
is the greatest common divisor of the lengths of its cycles, and so
![]() $p(\Gamma )$
is equal to the greatest common divisor of the lengths of its closed walks. A digraph
$p(\Gamma )$
is equal to the greatest common divisor of the lengths of its closed walks. A digraph
![]() $\Gamma $
is strong (or strongly connected) if for each
$\Gamma $
is strong (or strongly connected) if for each
![]() $u,v\in V(\Gamma )$
there is a path from u to v (and hence, also a path from v to u); it follows that every vertex of a nontrivial, strong digraph is contained in some cycle [Reference Harary, Norman and Cartwright9, p. 64]. A weak component (or weakly connected component) of a digraph
$u,v\in V(\Gamma )$
there is a path from u to v (and hence, also a path from v to u); it follows that every vertex of a nontrivial, strong digraph is contained in some cycle [Reference Harary, Norman and Cartwright9, p. 64]. A weak component (or weakly connected component) of a digraph
![]() $\Gamma $
is a maximal subdigraph of
$\Gamma $
is a maximal subdigraph of
![]() $\Gamma $
whose underlying graph is connected. A digraph is weak (or weakly connected) if it has exactly one weak component. A digraph
$\Gamma $
whose underlying graph is connected. A digraph is weak (or weakly connected) if it has exactly one weak component. A digraph
![]() $\Gamma $
is bipartite if there is a vertex partition
$\Gamma $
is bipartite if there is a vertex partition ![]() such that if
such that if
![]() $[u,v]\in A(\Gamma )$
then either
$[u,v]\in A(\Gamma )$
then either
![]() $u\in V_1$
and
$u\in V_1$
and
![]() $v \in V_2$
or
$v \in V_2$
or
![]() $u\in V_2$
and
$u\in V_2$
and
![]() $v \in V_1$
. A strong digraph is bipartite if and only if it has no odd length cycles [Reference Harary, Norman and Cartwright9, Theorem 6.14], that is, if and only if its period is even.
$v \in V_1$
. A strong digraph is bipartite if and only if it has no odd length cycles [Reference Harary, Norman and Cartwright9, Theorem 6.14], that is, if and only if its period is even.
The Cartesian product
![]() $\Gamma _1\square \Gamma _2$
of digraphs
$\Gamma _1\square \Gamma _2$
of digraphs
![]() $\Gamma _1,\Gamma _2$
is the digraph
$\Gamma _1,\Gamma _2$
is the digraph
![]() $\Gamma $
with
$\Gamma $
with
![]() ${V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)}$
and
${V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)}$
and
![]() $A(\Gamma ) = \{ [ (u,u'), (v,v') ]\ |\ [u,v]\in A(\Gamma _1), u'=v'~\mathrm {or} [u',v']\in A(\Gamma _2), u=v \}$
. The direct product
$A(\Gamma ) = \{ [ (u,u'), (v,v') ]\ |\ [u,v]\in A(\Gamma _1), u'=v'~\mathrm {or} [u',v']\in A(\Gamma _2), u=v \}$
. The direct product
![]() $\Gamma _1\times \Gamma _2$
of digraphs
$\Gamma _1\times \Gamma _2$
of digraphs
![]() $\Gamma _1,\Gamma _2$
is the digraph
$\Gamma _1,\Gamma _2$
is the digraph
![]() $\Gamma $
with
$\Gamma $
with
![]() $V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)$
and
$V(\Gamma )=V(\Gamma _1)\times V(\Gamma _2)$
and
![]() $A(\Gamma ) = \{ [ (u,u'), (v,v') ]\ |\ [u,v]\in A(\Gamma _1)~\mathrm {and}~[u',v']\in A(\Gamma _2)\}$
. Both graph products
$A(\Gamma ) = \{ [ (u,u'), (v,v') ]\ |\ [u,v]\in A(\Gamma _1)~\mathrm {and}~[u',v']\in A(\Gamma _2)\}$
. Both graph products
![]() $\square $
and
$\square $
and
![]() $\times $
are associative [Reference Hammack, Bang-Jensen and Gutin8].
$\times $
are associative [Reference Hammack, Bang-Jensen and Gutin8].
Given a finite group G with generating set S that does not contain the identity of G, the Cayley digraph
![]() $\mathrm {Cay}(G,S)$
is the digraph
$\mathrm {Cay}(G,S)$
is the digraph
![]() $\Gamma $
with
$\Gamma $
with
![]() $V(\Gamma )=G$
and arc set
$V(\Gamma )=G$
and arc set
Thus, every finite Cayley digraph is strong. The circulant digraph
![]() $\mathrm {circ}_n\{ d_1,\dots ,d_t\}$
, where
$\mathrm {circ}_n\{ d_1,\dots ,d_t\}$
, where
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq d_1,\dots ,d_t<n$
are distinct integers, is the digraph
$1\leq d_1,\dots ,d_t<n$
are distinct integers, is the digraph
![]() $\Gamma $
with
$\Gamma $
with
![]() ${V(\Gamma )=\{0,1,\dots ,n-1\}}$
and arcs
${V(\Gamma )=\{0,1,\dots ,n-1\}}$
and arcs
![]() $[i,i+d_j]$
for each
$[i,i+d_j]$
for each
![]() $0\leq i<n, 1\leq j\leq t$
(where the entries are taken
$0\leq i<n, 1\leq j\leq t$
(where the entries are taken
![]() $\bmod \,n$
) [Reference Ádám1]. It is weakly connected if and only if
$\bmod \,n$
) [Reference Ádám1]. It is weakly connected if and only if
![]() ${\mathrm {gcd}\{n,d_1,\dots ,d_t\}=1}$
, in which case it is strongly connected and is the Cayley digraph
${\mathrm {gcd}\{n,d_1,\dots ,d_t\}=1}$
, in which case it is strongly connected and is the Cayley digraph
![]() $\mathrm {Cay}(\mathbb {Z}_n, \{d_1,\dots ,d_t\})$
.
$\mathrm {Cay}(\mathbb {Z}_n, \{d_1,\dots ,d_t\})$
.
3 Digraph groups
First, we observe that if
![]() $\Gamma $
has weakly connected components
$\Gamma $
has weakly connected components
![]() $\Gamma _1, \dots , \Gamma _k$
with
$\Gamma _1, \dots , \Gamma _k$
with
![]() ${k\geq 2}$
, then the presentation
${k\geq 2}$
, then the presentation
![]() $P_{\Gamma} (R)$
decomposes as the disjoint union of the presentations
$P_{\Gamma} (R)$
decomposes as the disjoint union of the presentations
![]() $P_{\Gamma _1}(R),\dots , P_{\Gamma _k}(R)$
, so
$P_{\Gamma _1}(R),\dots , P_{\Gamma _k}(R)$
, so
![]() $G_{\Gamma} (R)$
is isomorphic to the free product
$G_{\Gamma} (R)$
is isomorphic to the free product
![]() $G_{\Gamma _1}(R)*\cdots * G_{\Gamma _k}(R)$
. Therefore, without loss of generality, in considering digraph groups
$G_{\Gamma _1}(R)*\cdots * G_{\Gamma _k}(R)$
. Therefore, without loss of generality, in considering digraph groups
![]() $G_{\Gamma} (R)$
, we may assume that
$G_{\Gamma} (R)$
, we may assume that
![]() $\Gamma $
is weak.
$\Gamma $
is weak.
Lemma 3.1 [Reference Pride17]
Let
![]() $\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free and let
$\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
![]() $G_{\Gamma} (R)$
is finite, then
$G_{\Gamma} (R)$
is finite, then
![]() $\alpha \neq 0, \beta \neq 0$
, and
$\alpha \neq 0, \beta \neq 0$
, and
![]() $a^\alpha =b^\beta $
in K.
$a^\alpha =b^\beta $
in K.
Proof By [Reference Pride17, Theorem 4], if K has Property
![]() $W_1$
(see [Reference Pride17] for the definition), then
$W_1$
(see [Reference Pride17] for the definition), then
![]() $G_{\Gamma} (R)$
is infinite, so we may assume that K does not satisfy Property
$G_{\Gamma} (R)$
is infinite, so we may assume that K does not satisfy Property
![]() $W_1$
. Then, by [Reference Pride17, Proposition, p. 248], we have
$W_1$
. Then, by [Reference Pride17, Proposition, p. 248], we have
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\beta \neq 0$
, and
$\beta \neq 0$
, and
![]() $a^\alpha =b^\beta $
in K (see [Reference Cuno and Williams7, p. 5] for further discussion on this point).
$a^\alpha =b^\beta $
in K (see [Reference Cuno and Williams7, p. 5] for further discussion on this point).
Lemma 3.2 Let
![]() $\Gamma $
be a digraph and let
$\Gamma $
be a digraph and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
![]() $a^\alpha =b^\beta $
in K, then
$a^\alpha =b^\beta $
in K, then
![]() $G_{\Gamma} (R)$
is a quotient of
$G_{\Gamma} (R)$
is a quotient of
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
, so, in particular, if
$G_{\Gamma} (a^\alpha b^{-\beta })$
, so, in particular, if
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
$G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
![]() $G_{\Gamma} (R) \cong G_{\Gamma} (a^\alpha b^{-\beta })$
.
$G_{\Gamma} (R) \cong G_{\Gamma} (a^\alpha b^{-\beta })$
.
Proof Since
![]() $a^\alpha =b^{\beta }$
in K, the presence of a relator
$a^\alpha =b^{\beta }$
in K, the presence of a relator
![]() $R(x_u,x_v)$
in
$R(x_u,x_v)$
in
![]() $P_{\Gamma} (R)$
implies that the relation
$P_{\Gamma} (R)$
implies that the relation
![]() $x_u^\alpha = x_v^{\beta }$
holds in
$x_u^\alpha = x_v^{\beta }$
holds in
![]() $G_{\Gamma} (R)$
. Therefore, the corresponding relators
$G_{\Gamma} (R)$
. Therefore, the corresponding relators
![]() $x_u^\alpha x_v^{-\beta }$
can be added to the defining presentation for
$x_u^\alpha x_v^{-\beta }$
can be added to the defining presentation for
![]() $G_{\Gamma} (R)$
, so
$G_{\Gamma} (R)$
, so
![]() $G_{\Gamma} (R)$
is a quotient of
$G_{\Gamma} (R)$
is a quotient of
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
. If
$G_{\Gamma} (a^\alpha b^{-\beta })$
. If
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
$G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
![]() $G_{\Gamma} (R)$
is abelian and so the relators
$G_{\Gamma} (R)$
is abelian and so the relators
![]() $R(x_u,x_v)$
are equivalent to the relators
$R(x_u,x_v)$
are equivalent to the relators
![]() $x_u^{\alpha }x_v^{-\beta }$
, so can be removed, that is,
$x_u^{\alpha }x_v^{-\beta }$
, so can be removed, that is,
![]() ${G_{\Gamma} (R)\cong G_{\Gamma} (a^\alpha b^{-\beta })}$
.
${G_{\Gamma} (R)\cong G_{\Gamma} (a^\alpha b^{-\beta })}$
.
Lemma 3.3 [Reference Pride17]
Let
![]() $\Gamma $
be a digraph that is not a tournament, and let
$\Gamma $
be a digraph that is not a tournament, and let
![]() $R(a,b)$
be a cyclically reduced word which has exponent sums
$R(a,b)$
be a cyclically reduced word which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively. If
$b^{-1}$
, respectively. If
![]() $G_{\Gamma} (R)$
is finite, then
$G_{\Gamma} (R)$
is finite, then
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
.
$\mathrm {gcd}\{\alpha ,\beta \}=1$
.
Proof Since
![]() $\Gamma $
is not a tournament, there exists a pair of vertices
$\Gamma $
is not a tournament, there exists a pair of vertices
![]() $u,v\in V(\Gamma )$
that are not connected by an arc. As in [Reference Pride17, p. 248] (or [Reference Cuno and Williams7, Proof of Lemma 3.3]), killing all generators of
$u,v\in V(\Gamma )$
that are not connected by an arc. As in [Reference Pride17, p. 248] (or [Reference Cuno and Williams7, Proof of Lemma 3.3]), killing all generators of
![]() $G_{\Gamma} (R)$
except
$G_{\Gamma} (R)$
except
![]() $x_u,x_v$
and then adjoining relators
$x_u,x_v$
and then adjoining relators
![]() $x_u^{d},x_v^{d}$
, where
$x_u^{d},x_v^{d}$
, where
![]() ${d=\mathrm {gcd}\{\alpha ,\beta \}}$
, gives that
${d=\mathrm {gcd}\{\alpha ,\beta \}}$
, gives that
![]() $G_{\Gamma} (R)$
maps onto the group
$G_{\Gamma} (R)$
maps onto the group
![]() $\langle {x_u,x_v}\ |\ {x_u^{d},x_v^{d}} \rangle \cong \mathbb {Z}_{d}*\mathbb {Z}_{d}$
, which is infinite if
$\langle {x_u,x_v}\ |\ {x_u^{d},x_v^{d}} \rangle \cong \mathbb {Z}_{d}*\mathbb {Z}_{d}$
, which is infinite if
![]() $d>1$
.
$d>1$
.
Lemma 3.4 Let
![]() $\Gamma $
be a digraph, and let
$\Gamma $
be a digraph, and let
![]() $R(a,b)$
be a cyclically reduced word which has exponent sums
$R(a,b)$
be a cyclically reduced word which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively. Then
$b^{-1}$
, respectively. Then
![]() $G_{\Gamma} (R)$
maps epimorphically to
$G_{\Gamma} (R)$
maps epimorphically to
![]() $\mathbb {Z}_{|\alpha -\beta |}$
. In particular, if
$\mathbb {Z}_{|\alpha -\beta |}$
. In particular, if
![]() $\alpha =\beta $
, then
$\alpha =\beta $
, then
![]() $G_{\Gamma} (R)$
is infinite.
$G_{\Gamma} (R)$
is infinite.
Proof Let
![]() $\phi :G_{\Gamma} (R)\rightarrow \mathbb {Z}_{|\alpha -\beta |}$
be given by
$\phi :G_{\Gamma} (R)\rightarrow \mathbb {Z}_{|\alpha -\beta |}$
be given by
![]() $\phi (x_v)=1\in \mathbb {Z}_{|\alpha -\beta |}$
for each
$\phi (x_v)=1\in \mathbb {Z}_{|\alpha -\beta |}$
for each
![]() $v\in V(\Gamma )$
. Then, for each relator
$v\in V(\Gamma )$
. Then, for each relator
![]() $R(x_u,x_v)$
of
$R(x_u,x_v)$
of
![]() $G_{\Gamma} (R)$
, we have
$G_{\Gamma} (R)$
, we have
![]() $\phi (R(x_u,x_v))=\alpha \cdot 1 -\beta \cdot 1 =0 \in \mathbb {Z}_{|\alpha -\beta |}$
, so
$\phi (R(x_u,x_v))=\alpha \cdot 1 -\beta \cdot 1 =0 \in \mathbb {Z}_{|\alpha -\beta |}$
, so
![]() $\phi $
is a homomorphism, and since
$\phi $
is a homomorphism, and since
![]() $\phi (x_v)=1$
for some
$\phi (x_v)=1$
for some
![]() $v\in V(\Gamma )$
, it is an epimorphism.
$v\in V(\Gamma )$
, it is an epimorphism.
Lemma 3.5 Let
![]() $\Gamma $
be a bipartite digraph and let
$\Gamma $
be a bipartite digraph and let
![]() $R(a,b)$
be a cyclically reduced word which has exponent sums
$R(a,b)$
be a cyclically reduced word which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and suppose
$b^{-1}$
, respectively, and suppose
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
. Then
$\mathrm {gcd}\{\alpha ,\beta \}=1$
. Then
![]() $G_{\Gamma} (R)$
maps epimorphically to
$G_{\Gamma} (R)$
maps epimorphically to
![]() $\mathbb {Z}_{|\alpha ^2-\beta ^2|}$
. In particular, if
$\mathbb {Z}_{|\alpha ^2-\beta ^2|}$
. In particular, if
![]() $\alpha =\pm \beta $
, then
$\alpha =\pm \beta $
, then
![]() $G_{\Gamma} (R)$
is infinite.
$G_{\Gamma} (R)$
is infinite.
Proof Suppose
![]() $\Gamma $
has vertex partition
$\Gamma $
has vertex partition ![]() . Let
. Let
![]() $\phi :G_{\Gamma} (R) \rightarrow \mathbb {Z}_{|\alpha ^2-\beta ^2|}$
be given by
$\phi :G_{\Gamma} (R) \rightarrow \mathbb {Z}_{|\alpha ^2-\beta ^2|}$
be given by
![]() $\phi (x_u)=\alpha $
if
$\phi (x_u)=\alpha $
if
![]() $u\in V_1$
and
$u\in V_1$
and
![]() $\phi (x_u)=\beta $
if
$\phi (x_u)=\beta $
if
![]() $u \in V_2$
. Then given an arc
$u \in V_2$
. Then given an arc
![]() $[u,v]$
of
$[u,v]$
of
![]() $G_{\Gamma} (R)$
, we have
$G_{\Gamma} (R)$
, we have
![]() $\phi (R(x_u,x_v))=\alpha ^2-\beta ^2=0$
if
$\phi (R(x_u,x_v))=\alpha ^2-\beta ^2=0$
if
![]() $u\in V_1$
and
$u\in V_1$
and
![]() ${\phi (R(x_u,x_v))=\alpha \beta -\beta \alpha =0}$
if
${\phi (R(x_u,x_v))=\alpha \beta -\beta \alpha =0}$
if
![]() $u\in V_2$
. Thus,
$u\in V_2$
. Thus,
![]() $\phi $
is a homomorphism. Since
$\phi $
is a homomorphism. Since
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
, there exist
$\mathrm {gcd}\{\alpha ,\beta \}=1$
, there exist
![]() $r,s\in \mathbb {Z}$
such that
$r,s\in \mathbb {Z}$
such that
![]() $r\alpha +s\beta =1$
, and so if
$r\alpha +s\beta =1$
, and so if
![]() $u \in V_1, v \in V_2$
, then
$u \in V_1, v \in V_2$
, then
![]() $\phi (x_u^rx_v^s)=r\alpha +s\beta =1\in \mathbb {Z}_{|\alpha ^2-\beta ^2|}$
, so
$\phi (x_u^rx_v^s)=r\alpha +s\beta =1\in \mathbb {Z}_{|\alpha ^2-\beta ^2|}$
, so
![]() $\phi $
is an epimorphism.
$\phi $
is an epimorphism.
Lemma 3.6 Let
![]() $\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free, and let
$\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free, and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and suppose
$b^{-1}$
, respectively, and suppose
![]() $\alpha =-\beta $
. Then
$\alpha =-\beta $
. Then
![]() ${G=G_{\Gamma} (R)}$
is finite if and only if
${G=G_{\Gamma} (R)}$
is finite if and only if
![]() $\alpha =-\beta = \pm 1$
,
$\alpha =-\beta = \pm 1$
,
![]() $a^\alpha =b^\beta $
in K, and
$a^\alpha =b^\beta $
in K, and
![]() $\Gamma $
is not bipartite, in which case
$\Gamma $
is not bipartite, in which case
![]() $G\cong \mathbb {Z}_2$
.
$G\cong \mathbb {Z}_2$
.
Proof Suppose G is finite. Then Lemma 3.1 implies
![]() $\alpha \neq 0, \beta \neq 0$
, and
$\alpha \neq 0, \beta \neq 0$
, and
![]() $a^\alpha =b^\beta $
in K, and Lemma 3.3 implies
$a^\alpha =b^\beta $
in K, and Lemma 3.3 implies
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
, so
$\mathrm {gcd}\{\alpha ,\beta \}=1$
, so
![]() $\alpha =-\beta =\pm 1$
. Moreover,
$\alpha =-\beta =\pm 1$
. Moreover,
![]() $\Gamma $
is not bipartite by Lemma 3.5. Under these conditions
$\Gamma $
is not bipartite by Lemma 3.5. Under these conditions
![]() $a=b^{-1}$
in K and so, given an arc
$a=b^{-1}$
in K and so, given an arc
![]() $[u,v]\in A(\Gamma )$
, we have
$[u,v]\in A(\Gamma )$
, we have
![]() $x_u=x_v^{-1}$
in G. Fix a vertex
$x_u=x_v^{-1}$
in G. Fix a vertex
![]() $w\in V(\Gamma )$
. Then, since the underlying graph of
$w\in V(\Gamma )$
. Then, since the underlying graph of
![]() $\Gamma $
is connected, for any
$\Gamma $
is connected, for any
![]() $v\in V(\Gamma )$
we have either
$v\in V(\Gamma )$
we have either
![]() $x_v=x_w$
or
$x_v=x_w$
or
![]() $x_v=x_w^{-1}$
. Therefore, G is cyclic. Since
$x_v=x_w^{-1}$
. Therefore, G is cyclic. Since
![]() $\Gamma $
is not bipartite, there is an odd length cycle
$\Gamma $
is not bipartite, there is an odd length cycle
![]() $1\rightarrow 2\rightarrow 3\rightarrow \dots \rightarrow r\rightarrow 1$
, say. Then
$1\rightarrow 2\rightarrow 3\rightarrow \dots \rightarrow r\rightarrow 1$
, say. Then
![]() $x_1=x_2^{-1}=x_3=\dots =x_{r-1}^{-1}=x_r=x_1^{-1}$
, so
$x_1=x_2^{-1}=x_3=\dots =x_{r-1}^{-1}=x_r=x_1^{-1}$
, so
![]() $x_1^2=1$
. Moreover, each generator of G is equal to any other generator or its inverse, so G is generated by
$x_1^2=1$
. Moreover, each generator of G is equal to any other generator or its inverse, so G is generated by
![]() $x_1$
, which satisfies the relation
$x_1$
, which satisfies the relation
![]() $x_1^2=1$
, that is, G is cyclic of order at most 2. Then, by Lemma 3.4, G maps onto
$x_1^2=1$
, that is, G is cyclic of order at most 2. Then, by Lemma 3.4, G maps onto
![]() $\mathbb {Z}_2$
, so
$\mathbb {Z}_2$
, so
![]() $G\cong \mathbb {Z}_2$
.
$G\cong \mathbb {Z}_2$
.
By Lemma 3.6, we may assume
![]() $\alpha \neq -\beta $
. In this situation, we summarize Lemmas 3.1–3.4 in the following result.
$\alpha \neq -\beta $
. In this situation, we summarize Lemmas 3.1–3.4 in the following result.
Theorem 3.7 Let
![]() $\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free and let
$\Gamma $
be a nontrivial, weak digraph that is digon-free and triangle-free and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, where
$b^{-1}$
, respectively, where
![]() $\alpha \neq -\beta $
, and let
$\alpha \neq -\beta $
, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. If
![]() $G_{\Gamma} (R)$
is finite, then
$G_{\Gamma} (R)$
is finite, then
![]() $\alpha \neq 0, \beta \neq 0$
,
$\alpha \neq 0, \beta \neq 0$
,
![]() $\alpha \neq \beta $
,
$\alpha \neq \beta $
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
, and
$\mathrm {gcd}\{\alpha ,\beta \}=1$
, and
![]() $a^\alpha =b^\beta $
in K, in which case
$a^\alpha =b^\beta $
in K, in which case
![]() $G_{\Gamma} (R)$
is a quotient of
$G_{\Gamma} (R)$
is a quotient of
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
, so, in particular, if
$G_{\Gamma} (a^\alpha b^{-\beta })$
, so, in particular, if
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
$G_{\Gamma} (a^\alpha b^{-\beta })$
is abelian, then
![]() $G_{\Gamma} (R) \cong G_{\Gamma} (a^\alpha b^{-\beta })$
.
$G_{\Gamma} (R) \cong G_{\Gamma} (a^\alpha b^{-\beta })$
.
4 Strong digraph groups
In this section, we prove Theorem 1.2.
Lemma 4.1 Let
![]() $\Gamma $
be a digraph, and let
$\Gamma $
be a digraph, and let
![]() $G=G_{\Gamma} (a^{\alpha } b ^{-\beta })$
where
$G=G_{\Gamma} (a^{\alpha } b ^{-\beta })$
where
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
. If v is a vertex of a cycle of length
$\mathrm {gcd}\{\alpha ,\beta \}=1$
. If v is a vertex of a cycle of length
![]() $\Delta $
in
$\Delta $
in
![]() $\Gamma $
, then
$\Gamma $
, then
![]() $x_v^{|\alpha ^\Delta - \beta ^\Delta |}=1$
in G.
$x_v^{|\alpha ^\Delta - \beta ^\Delta |}=1$
in G.
Proof This is essentially stated implicitly in [Reference Pride17, p. 248], and proofs are given in [Reference Cuno and Williams7, Lemma 3.4] and [Reference Bogley and Williams3, Lemma 3.4].
Lemma 4.2 Let
![]() $\Gamma $
be a digraph, and let
$\Gamma $
be a digraph, and let
![]() $G=G_{\Gamma} (a^{\alpha } b^{-\beta })$
where
$G=G_{\Gamma} (a^{\alpha } b^{-\beta })$
where
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
. Let
$\mathrm {gcd}\{\alpha ,\beta \}=1$
. Let
![]() $u\in V(\Gamma )$
be a vertex of some cycle, and suppose there is a path from u to a vertex w. Then the generator
$u\in V(\Gamma )$
be a vertex of some cycle, and suppose there is a path from u to a vertex w. Then the generator
![]() $x_u$
of G is equal to a power of the generator
$x_u$
of G is equal to a power of the generator
![]() $x_w$
.
$x_w$
.
Proof Label the path from u to w as
![]() $u=1 \rightarrow 2 \rightarrow 3 \rightarrow \cdots \rightarrow (n-1) \rightarrow n=w$
. First, consider the arc
$u=1 \rightarrow 2 \rightarrow 3 \rightarrow \cdots \rightarrow (n-1) \rightarrow n=w$
. First, consider the arc
![]() $[1,2]$
. Since
$[1,2]$
. Since
![]() $1$
is the vertex of some cycle, of length
$1$
is the vertex of some cycle, of length
![]() $\Delta $
, say, Lemma 4.1 implies
$\Delta $
, say, Lemma 4.1 implies
![]() $x_1^\gamma =1$
, where
$x_1^\gamma =1$
, where
![]() $\gamma =|\alpha ^\Delta - \beta ^\Delta |$
. Now
$\gamma =|\alpha ^\Delta - \beta ^\Delta |$
. Now
![]() $\mathrm {gcd}\{\alpha ,\gamma \}=1$
, so there exist
$\mathrm {gcd}\{\alpha ,\gamma \}=1$
, so there exist
![]() $r,s\in \mathbb {Z}$
such that
$r,s\in \mathbb {Z}$
such that
![]() $r\alpha +s \gamma =1$
, so
$r\alpha +s \gamma =1$
, so
![]() $r\alpha \equiv 1 \bmod \gamma $
. Moreover, there is a relation
$r\alpha \equiv 1 \bmod \gamma $
. Moreover, there is a relation
![]() $x_1^\alpha =x_2^\beta $
in
$x_1^\alpha =x_2^\beta $
in
![]() $\Gamma $
, so
$\Gamma $
, so
Therefore,
![]() $x_1$
is equal to a power of
$x_1$
is equal to a power of
![]() $x_2$
. Moreover,
$x_2$
. Moreover,
![]() $x_1^\gamma =1$
, so
$x_1^\gamma =1$
, so
![]() $(x_2^{r\beta })^\gamma =1$
, i.e.,
$(x_2^{r\beta })^\gamma =1$
, i.e.,
![]() $x_2^{r\beta \gamma }=1$
. But also
$x_2^{r\beta \gamma }=1$
. But also
![]() $x_1^\alpha =x_2^\beta $
so
$x_1^\alpha =x_2^\beta $
so
![]() $(x_2^{r\beta })^\alpha =x_2^\beta $
, so
$(x_2^{r\beta })^\alpha =x_2^\beta $
, so
![]() $x_2^{(1-r\alpha )\beta }=1$
, i.e.,
$x_2^{(1-r\alpha )\beta }=1$
, i.e.,
![]() $x_2^{s\beta \gamma }=1$
. Thus,
$x_2^{s\beta \gamma }=1$
. Thus,
![]() $x_2^{(r\beta \gamma ,s\beta \gamma )}=1$
, i.e.,
$x_2^{(r\beta \gamma ,s\beta \gamma )}=1$
, i.e.,
![]() $x_2^{|\beta \gamma |}=1$
. (The argument in this paragraph is that of [Reference Cuno and Williams7, Proof of Lemma 3.1].)
$x_2^{|\beta \gamma |}=1$
. (The argument in this paragraph is that of [Reference Cuno and Williams7, Proof of Lemma 3.1].)
Now consider the arc
![]() $[2,3]$
. Let
$[2,3]$
. Let
![]() $\gamma '=\beta \gamma $
. Noting that
$\gamma '=\beta \gamma $
. Noting that
![]() $\mathrm {gcd}\{\alpha ,\gamma '\}=1$
, repeating the argument of the previous paragraph gives that
$\mathrm {gcd}\{\alpha ,\gamma '\}=1$
, repeating the argument of the previous paragraph gives that
![]() $x_2$
is equal to a power of
$x_2$
is equal to a power of
![]() $x_3$
and
$x_3$
and
![]() ${x_3^{|\beta \gamma '|}=1}$
, that is,
${x_3^{|\beta \gamma '|}=1}$
, that is,
![]() $x_3^{|\beta ^2 \gamma |}=1$
. Continuing in this way, we see that for each
$x_3^{|\beta ^2 \gamma |}=1$
. Continuing in this way, we see that for each
![]() $1\leq i<n$
the generator
$1\leq i<n$
the generator
![]() $x_i$
is equal to a power of
$x_i$
is equal to a power of
![]() $x_{i+1}$
and
$x_{i+1}$
and
![]() $x_i^{|\beta ^{i-1}\gamma |}=1$
. Therefore,
$x_i^{|\beta ^{i-1}\gamma |}=1$
. Therefore,
![]() $x_1$
is equal to a power of
$x_1$
is equal to a power of
![]() $x_n$
, that is,
$x_n$
, that is,
![]() $x_u$
is equal to a power of
$x_u$
is equal to a power of
![]() $x_w$
, as required.
$x_w$
, as required.
Lemma 4.3 Let
![]() $\Gamma $
be a nontrivial, strong digraph of period p, and let
$\Gamma $
be a nontrivial, strong digraph of period p, and let
![]() $\alpha ,\beta \in \mathbb {Z}$
satisfy
$\alpha ,\beta \in \mathbb {Z}$
satisfy
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\beta \neq 0$
,
$\beta \neq 0$
,
![]() $\alpha \neq \pm \beta $
,
$\alpha \neq \pm \beta $
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
. Then
$\mathrm {gcd}\{\alpha ,\beta \}=1$
. Then
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
is finite and cyclic, of order dividing
$G_{\Gamma} (a^\alpha b^{-\beta })$
is finite and cyclic, of order dividing
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
Proof Fix a vertex
![]() $w\in V(\Gamma )$
. Since
$w\in V(\Gamma )$
. Since
![]() $\Gamma $
is nontrivial and strong, for every vertex
$\Gamma $
is nontrivial and strong, for every vertex
![]() $u\in V(\Gamma )$
, u is a vertex of some cycle and there is a walk from u to w. Therefore, by Lemma 4.2, the generator
$u\in V(\Gamma )$
, u is a vertex of some cycle and there is a walk from u to w. Therefore, by Lemma 4.2, the generator
![]() $x_u$
is equal to some power of
$x_u$
is equal to some power of
![]() $x_w$
. Therefore, every generator of G is equal to some power of
$x_w$
. Therefore, every generator of G is equal to some power of
![]() $x_w$
, so G is cyclic, generated by
$x_w$
, so G is cyclic, generated by
![]() $x_w$
. Since the choice of w was arbitrary, G is cyclic and generated by
$x_w$
. Since the choice of w was arbitrary, G is cyclic and generated by
![]() $x_v$
for any
$x_v$
for any
![]() $v \in V(\Gamma )$
and, by Lemma 4.1, if
$v \in V(\Gamma )$
and, by Lemma 4.1, if
![]() $\Delta $
is the length of any cycle of which v is a vertex,
$\Delta $
is the length of any cycle of which v is a vertex,
![]() $x_v^{|\alpha ^\Delta -\beta ^\Delta |}=1$
in G. That is, G is cyclic of order dividing
$x_v^{|\alpha ^\Delta -\beta ^\Delta |}=1$
in G. That is, G is cyclic of order dividing
![]() $f(\Delta )=|\alpha ^\Delta -\beta ^\Delta |$
. Applying this observation to every vertex
$f(\Delta )=|\alpha ^\Delta -\beta ^\Delta |$
. Applying this observation to every vertex
![]() $v\in V(\Gamma )$
and every cycle of
$v\in V(\Gamma )$
and every cycle of
![]() $\Gamma $
of which v is a vertex, we see that G is cyclic of order dividing
$\Gamma $
of which v is a vertex, we see that G is cyclic of order dividing
![]() $\mathrm {gcd} \{ f(\Delta )\ |\ \Delta ~\mathrm {is~the~length~of~some~cycle~of}~\Gamma \}$
. That is, G is cyclic of order dividing
$\mathrm {gcd} \{ f(\Delta )\ |\ \Delta ~\mathrm {is~the~length~of~some~cycle~of}~\Gamma \}$
. That is, G is cyclic of order dividing
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
Lemma 4.4 Let
![]() $\Gamma $
be a strong digraph of period
$\Gamma $
be a strong digraph of period
![]() $p\geq 2$
, let
$p\geq 2$
, let
![]() $\Lambda $
be the cycle of length p, and let
$\Lambda $
be the cycle of length p, and let
![]() $R(a,b)$
be a cyclically reduced word. Then
$R(a,b)$
be a cyclically reduced word. Then
![]() $G_{\Gamma} (R)$
maps epimorphically to
$G_{\Gamma} (R)$
maps epimorphically to
![]() $G_{\Lambda} (R)$
.
$G_{\Lambda} (R)$
.
Proof (In this proof, subscripts of
![]() $v_*,V_*$
, and
$v_*,V_*$
, and
![]() $y_*$
terms are to be taken
$y_*$
terms are to be taken
![]() $\bmod p$
.) By [Reference Bang-Jensen and Gutin2, Theorem 10.5.1], there exists a vertex partition
$\bmod p$
.) By [Reference Bang-Jensen and Gutin2, Theorem 10.5.1], there exists a vertex partition ![]() such that if
such that if
![]() $[u,v]\in A(\Gamma )$
then
$[u,v]\in A(\Gamma )$
then
![]() $u \in V_i$
and
$u \in V_i$
and
![]() $v \in V_{i+1}$
for some
$v \in V_{i+1}$
for some
![]() $0\leq i<p$
. By adjoining all relators
$0\leq i<p$
. By adjoining all relators
![]() $R(x_{v_i},x_{v_{i+1}})$
, where
$R(x_{v_i},x_{v_{i+1}})$
, where
![]() $v_i\in V_i, v_{i+1}\in V_{i+1}$
to the defining presentation for
$v_i\in V_i, v_{i+1}\in V_{i+1}$
to the defining presentation for
![]() $G=G_{\Gamma} (R)$
, we see that G maps onto
$G=G_{\Gamma} (R)$
, we see that G maps onto
For each
![]() $0\leq i<p$
, equating all generators
$0\leq i<p$
, equating all generators
![]() $x_{v_i}$
(
$x_{v_i}$
(
![]() $v_i\in V_i$
), and introducing generators
$v_i\in V_i$
), and introducing generators
![]() $y_i=x_{v_i}$
, we see that H maps onto
$y_i=x_{v_i}$
, we see that H maps onto
 $$\begin{align*} K&= \Bigg \langle \begin{array}{l} {x_{v_i}\ (v_i \in V_i, 0\leq i<p),}\\{y_i\ (0\leq i<p)} \end{array} \Bigg | \begin{array}{l} {R(x_{v_i}, x_{v_{i+1}})\ (v_i \in V_i, v_{i+1} \in V_{i+1}, 0\leq i<p),}\\{y_i=x_{v_i} \ (v_i \in V_i, 0\leq i<p)} \end{array} \Bigg \rangle\\ &= \langle {y_i\ (0\leq i<p)}\ |\ {R(y_i,y_{i+1})\ (0\leq i<p)} \rangle\\ &= G_{\Lambda} (R), \end{align*}$$
$$\begin{align*} K&= \Bigg \langle \begin{array}{l} {x_{v_i}\ (v_i \in V_i, 0\leq i<p),}\\{y_i\ (0\leq i<p)} \end{array} \Bigg | \begin{array}{l} {R(x_{v_i}, x_{v_{i+1}})\ (v_i \in V_i, v_{i+1} \in V_{i+1}, 0\leq i<p),}\\{y_i=x_{v_i} \ (v_i \in V_i, 0\leq i<p)} \end{array} \Bigg \rangle\\ &= \langle {y_i\ (0\leq i<p)}\ |\ {R(y_i,y_{i+1})\ (0\leq i<p)} \rangle\\ &= G_{\Lambda} (R), \end{align*}$$
where
![]() $V(\Lambda )=\{ 0,1,\dots ,p-1 \}$
and
$V(\Lambda )=\{ 0,1,\dots ,p-1 \}$
and
![]() $A(\Lambda )=\{[i,i+1]\ |\ 0\leq i<p\}$
.
$A(\Lambda )=\{[i,i+1]\ |\ 0\leq i<p\}$
.
We can now prove Theorem 1.2.
Proof of Theorem 1.2
Suppose first
![]() $\alpha =-\beta $
. Then, by Lemma 3.6,
$\alpha =-\beta $
. Then, by Lemma 3.6,
![]() $G=G_{\Gamma} (R)$
is finite if and only if
$G=G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha =\pm 1$
,
$\alpha =\pm 1$
,
![]() $\Gamma $
is not bipartite, and
$\Gamma $
is not bipartite, and
![]() $a^\alpha =b^\beta $
in K, in which case
$a^\alpha =b^\beta $
in K, in which case
![]() $G\cong \mathbb {Z}_2$
. Equivalently, G is finite if and only if
$G\cong \mathbb {Z}_2$
. Equivalently, G is finite if and only if
![]() $\alpha \neq 0, \beta \neq 0$
,
$\alpha \neq 0, \beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
, and
$\alpha ^p\neq \beta ^p$
, and
![]() $a^\alpha =b^\beta $
in K, in which case
$a^\alpha =b^\beta $
in K, in which case
![]() $G\cong \mathbb {Z}_{|\alpha ^p-\beta ^p|}$
.
$G\cong \mathbb {Z}_{|\alpha ^p-\beta ^p|}$
.
Suppose then
![]() $\alpha \neq -\beta $
. If G is finite, then Theorem 3.7 implies
$\alpha \neq -\beta $
. If G is finite, then Theorem 3.7 implies
![]() $\alpha \neq 0,\beta \neq 0, \alpha \neq \beta $
(equivalently,
$\alpha \neq 0,\beta \neq 0, \alpha \neq \beta $
(equivalently,
![]() $\alpha ^p \neq \beta ^p$
),
$\alpha ^p \neq \beta ^p$
),
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
, and
$\mathrm {gcd}\{\alpha ,\beta \}=1$
, and
![]() $a^\alpha =b^\beta $
in K. Under these conditions, Lemma 4.3 implies that
$a^\alpha =b^\beta $
in K. Under these conditions, Lemma 4.3 implies that
![]() $G_{\Gamma} (a^\alpha b^{-\beta })$
is finite and cyclic of order dividing
$G_{\Gamma} (a^\alpha b^{-\beta })$
is finite and cyclic of order dividing
![]() $\gamma =|\alpha ^p-\beta ^p|$
. Then
$\gamma =|\alpha ^p-\beta ^p|$
. Then
![]() $G\cong G_{\Gamma} (a^\alpha b^{-\beta })$
by Theorem 3.7. We now show that G maps epimorphically to
$G\cong G_{\Gamma} (a^\alpha b^{-\beta })$
by Theorem 3.7. We now show that G maps epimorphically to
![]() $\mathbb {Z}_\gamma $
. If
$\mathbb {Z}_\gamma $
. If
![]() $p=1$
, this follows from Lemma 3.4, so assume
$p=1$
, this follows from Lemma 3.4, so assume
![]() $p\geq 2$
. By Lemma 4.4,
$p\geq 2$
. By Lemma 4.4,
![]() $G=G_{\Gamma} (a^\alpha b^{-\beta })$
maps epimorphically to
$G=G_{\Gamma} (a^\alpha b^{-\beta })$
maps epimorphically to
![]() $G_{\Lambda} (a^\alpha b^{-\beta })$
, where
$G_{\Lambda} (a^\alpha b^{-\beta })$
, where
![]() $\Lambda $
is the cycle of length p. But
$\Lambda $
is the cycle of length p. But
![]() $G_{\Lambda} (a^\alpha b^{-\beta })\cong \mathbb {Z}_\gamma $
by [Reference Pride17, p. 248] (or [Reference Cuno and Williams7, Lemma 3.4], [Reference Bogley and Williams3, Lemma 3.4]). Thus,
$G_{\Lambda} (a^\alpha b^{-\beta })\cong \mathbb {Z}_\gamma $
by [Reference Pride17, p. 248] (or [Reference Cuno and Williams7, Lemma 3.4], [Reference Bogley and Williams3, Lemma 3.4]). Thus,
![]() $G\cong \mathbb {Z}_\gamma $
, as required.
$G\cong \mathbb {Z}_\gamma $
, as required.
5 Applications
In this section, we obtain corollaries to Theorem 1.2 for particular types of strong digraphs.
5.1 A Cayley digraph
We consider the Cayley digraph of the generalized quaternion group
with respect to the generating set
![]() $\{c,d\}$
.
$\{c,d\}$
.
Lemma 5.1 Let
![]() $\Gamma = \mathrm {Cay}(Q_{2n},\{c,d\})$
where
$\Gamma = \mathrm {Cay}(Q_{2n},\{c,d\})$
where
![]() $n\geq 2$
. Then
$n\geq 2$
. Then
![]() $\Gamma $
is digon-free and triangle-free and the period
$\Gamma $
is digon-free and triangle-free and the period
![]() $p(\Gamma )=\mathrm {gcd}\{n,2\}$
.
$p(\Gamma )=\mathrm {gcd}\{n,2\}$
.
Proof Since
![]() $c^2, d^2, c^3, d^3, c^2d^{\pm 1}, d^2c^{\pm 1}\neq e$
in
$c^2, d^2, c^3, d^3, c^2d^{\pm 1}, d^2c^{\pm 1}\neq e$
in
![]() $Q_{2n}$
(where e denotes the identity) the digraph
$Q_{2n}$
(where e denotes the identity) the digraph
![]() $\Gamma $
is digon-free and triangle-free. It contains the following cycles:
$\Gamma $
is digon-free and triangle-free. It contains the following cycles:
-
•
 $e\rightarrow d\rightarrow {d^2}\rightarrow {d^3}\rightarrow {d^4}={c^{2n}}=e$
,
$e\rightarrow d\rightarrow {d^2}\rightarrow {d^3}\rightarrow {d^4}={c^{2n}}=e$
, -
•
 $e \rightarrow c \rightarrow {c^2} \rightarrow \cdots \rightarrow {c^n} \rightarrow {c^nd} \rightarrow {c^nd^2}= {c^nc^n}={c^{2n}}=e$
,
$e \rightarrow c \rightarrow {c^2} \rightarrow \cdots \rightarrow {c^n} \rightarrow {c^nd} \rightarrow {c^nd^2}= {c^nc^n}={c^{2n}}=e$
, -
•
 ${e}\rightarrow {c}\rightarrow {c^2}\rightarrow \cdots \rightarrow {c^{2n-1}}\rightarrow {c^{2n-1}d}\rightarrow {c^{2n-1}dc} = {c^{2n-2}d}\rightarrow {c^{2n-2}dc} = {c^{2n-3} d}\rightarrow \cdots \rightarrow {c^nd}\rightarrow {c^nd^2} ={c^nc^n} = {c^{2n}} ={e}$
,
${e}\rightarrow {c}\rightarrow {c^2}\rightarrow \cdots \rightarrow {c^{2n-1}}\rightarrow {c^{2n-1}d}\rightarrow {c^{2n-1}dc} = {c^{2n-2}d}\rightarrow {c^{2n-2}dc} = {c^{2n-3} d}\rightarrow \cdots \rightarrow {c^nd}\rightarrow {c^nd^2} ={c^nc^n} = {c^{2n}} ={e}$
,
of lengths
![]() $4,n+2,3n$
, respectively, and so
$4,n+2,3n$
, respectively, and so
![]() $p=p(\Gamma )$
divides
$p=p(\Gamma )$
divides
![]() $\mathrm {gcd}\{4,n+2,3n\}$
, so
$\mathrm {gcd}\{4,n+2,3n\}$
, so
![]() $p=1$
if n is odd and
$p=1$
if n is odd and
![]() $p|2$
if n is even. If n is even, then
$p|2$
if n is even. If n is even, then
![]() $\Gamma $
is bipartite with vertex partition
$\Gamma $
is bipartite with vertex partition
and so
![]() $\Gamma $
has no odd length cycles and hence
$\Gamma $
has no odd length cycles and hence
![]() $p=2$
.
$p=2$
.
Noting that Cayley digraphs are strong, we obtain the following.
Corollary 5.2 Let
![]() $\Gamma = \mathrm {Cay}(Q_{2n},\{c,d\})$
where
$\Gamma = \mathrm {Cay}(Q_{2n},\{c,d\})$
where
![]() $n\geq 2$
, let
$n\geq 2$
, let
![]() $p=\mathrm {gcd}\{n,2\}$
, and let
$p=\mathrm {gcd}\{n,2\}$
, and let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() $G=G_{\Gamma} (R)$
is finite if and only if
$G=G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha \neq 0, \beta \neq 0$
,
$\alpha \neq 0, \beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
,
$\alpha ^p\neq \beta ^p$
,
![]() $a^\alpha =b^\beta $
in K, in which case G is cyclic of order
$a^\alpha =b^\beta $
in K, in which case G is cyclic of order
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
5.2 Circulant digraphs
Lemma 5.3 Let
![]() $\Gamma = \mathrm {circ}_n\{d_1,\dots ,d_t\}$
, where
$\Gamma = \mathrm {circ}_n\{d_1,\dots ,d_t\}$
, where
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq d_i<n$
for each
$1\leq d_i<n$
for each
![]() $1\leq i\leq t$
, and where
$1\leq i\leq t$
, and where
![]() $\mathrm {gcd}\{n,d_1,\dots ,d_t\}=1$
. Then
$\mathrm {gcd}\{n,d_1,\dots ,d_t\}=1$
. Then
![]() $p(\Gamma )=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
.
$p(\Gamma )=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
.
Proof Let
![]() $p=p(\Gamma )$
and
$p=p(\Gamma )$
and
![]() $r=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
. Observe that
$r=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
. Observe that
so there is a closed walk with
![]() $(n-d_2)$
arcs corresponding to the generator
$(n-d_2)$
arcs corresponding to the generator
![]() $d_1$
and
$d_1$
and
![]() $d_1$
arcs corresponding to the generator
$d_1$
arcs corresponding to the generator
![]() $d_2$
and 0 arcs corresponding to the remaining generators (and so has length
$d_2$
and 0 arcs corresponding to the remaining generators (and so has length
![]() $n+d_1-d_2$
). Similarly, there are closed walks of lengths
$n+d_1-d_2$
). Similarly, there are closed walks of lengths
![]() $n+d_1-d_3, \dots , n+d_1-d_t$
. Also, there is a closed walk of length n, consisting of
$n+d_1-d_3, \dots , n+d_1-d_t$
. Also, there is a closed walk of length n, consisting of
![]() $d_1$
arcs. Therefore, p divides
$d_1$
arcs. Therefore, p divides
![]() $\mathrm {gcd}\{ n,n+d_1-d_2,n+d_1-d_3,\dots , n+d_1-d_t\}=r$
.
$\mathrm {gcd}\{ n,n+d_1-d_2,n+d_1-d_3,\dots , n+d_1-d_t\}=r$
.
Consider a cycle of length l which has
![]() $l_i$
arcs corresponding to the generator
$l_i$
arcs corresponding to the generator
![]() $d_i$
, for each
$d_i$
, for each
![]() $1\leq i\leq t$
. Then
$1\leq i\leq t$
. Then
![]() $l=l_1+\dots + l_t$
and
$l=l_1+\dots + l_t$
and
![]() $\sum _{j=1}^t l_jd_j\equiv 0\bmod n$
, and hence
$\sum _{j=1}^t l_jd_j\equiv 0\bmod n$
, and hence
![]() $\sum _{j=1}^t l_jd_j\equiv 0\bmod r$
, so (since
$\sum _{j=1}^t l_jd_j\equiv 0\bmod r$
, so (since
![]() $d_j\equiv d_1 \bmod r$
for each
$d_j\equiv d_1 \bmod r$
for each
![]() $1\leq j\leq t$
) we have
$1\leq j\leq t$
) we have
![]() $\sum _{j=1}^t l_jd_1\equiv 0\bmod r$
. That is,
$\sum _{j=1}^t l_jd_1\equiv 0\bmod r$
. That is,
![]() $l d_1\equiv 0 \bmod r$
. Now, if
$l d_1\equiv 0 \bmod r$
. Now, if
![]() $\delta |r$
and
$\delta |r$
and
![]() $\delta |d_1$
, then
$\delta |d_1$
, then
![]() $\delta |d_2,\dots ,d_t$
so
$\delta |d_2,\dots ,d_t$
so
![]() $\delta |(n,d_1,\dots ,d_t)=1$
, so
$\delta |(n,d_1,\dots ,d_t)=1$
, so
![]() $\delta =1$
. Thus,
$\delta =1$
. Thus,
![]() $\mathrm {gcd}\{r,d_1\}=1$
, and so
$\mathrm {gcd}\{r,d_1\}=1$
, and so
![]() $l\equiv 0 \bmod r$
. Hence, r divides the length of any cycle in
$l\equiv 0 \bmod r$
. Hence, r divides the length of any cycle in
![]() $\Gamma $
, and so r divides p. Hence
$\Gamma $
, and so r divides p. Hence
![]() $p=r$
.
$p=r$
.
Noting that
![]() $\mathrm {circ}_n\{d_1,\dots ,d_t\}$
is digon-free and triangle-free if and only if
$\mathrm {circ}_n\{d_1,\dots ,d_t\}$
is digon-free and triangle-free if and only if
![]() ${d_i + d_j \not \equiv 0}$
and
${d_i + d_j \not \equiv 0}$
and
![]() $d_i+ d_j + d_k \not \equiv 0 \bmod n$
for each
$d_i+ d_j + d_k \not \equiv 0 \bmod n$
for each
![]() $1\leq i,j,k\leq t$
and that circulant digraphs are Cayley digraphs, and hence strong, we obtain the following.
$1\leq i,j,k\leq t$
and that circulant digraphs are Cayley digraphs, and hence strong, we obtain the following.
Corollary 5.4 Let
![]() $\mathrm {circ}_n\{d_1,\dots ,d_t\}$
, where
$\mathrm {circ}_n\{d_1,\dots ,d_t\}$
, where
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $1\leq d_i<n$
for each
$1\leq d_i<n$
for each
![]() $1\leq i\leq t$
, and where
$1\leq i\leq t$
, and where
![]() $\{d_1,\dots ,d_t\}$
is a generating set for
$\{d_1,\dots ,d_t\}$
is a generating set for
![]() $\mathbb {Z}_n$
and suppose
$\mathbb {Z}_n$
and suppose
![]() $d_i + d_j \not \equiv 0$
and
$d_i + d_j \not \equiv 0$
and
![]() $d_i+ d_j + d_k \not \equiv 0 \bmod n$
for each
$d_i+ d_j + d_k \not \equiv 0 \bmod n$
for each
![]() $1\leq i,j,k\leq t$
, and let
$1\leq i,j,k\leq t$
, and let
![]() $p=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
. Let
$p=\mathrm {gcd}\{n,d_1-d_2,d_1-d_3,\dots , d_1-d_t\}$
. Let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() ${G=G_{\Gamma} (R)}$
is finite if and only if
${G=G_{\Gamma} (R)}$
is finite if and only if
![]() $\alpha \neq 0, \beta \neq 0$
,
$\alpha \neq 0, \beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
,
$\alpha ^p\neq \beta ^p$
,
![]() $a^\alpha =b^\beta $
in K, in which case G is cyclic of order
$a^\alpha =b^\beta $
in K, in which case G is cyclic of order
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
5.3 Cartesian products of strong digraphs
Lemma 5.5 Let
![]() $\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
be the Cartesian product of digon-free and triangle-free strong digraphs
$\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
be the Cartesian product of digon-free and triangle-free strong digraphs
![]() $\Gamma _1,\dots ,\Gamma _t$
with periods
$\Gamma _1,\dots ,\Gamma _t$
with periods
![]() $p_1, \dots , p_t$
, respectively. Then
$p_1, \dots , p_t$
, respectively. Then
![]() $\Gamma $
is strong, digon-free, and triangle-free, with period
$\Gamma $
is strong, digon-free, and triangle-free, with period
![]() $p(\Gamma )=\mathrm {gcd}\{p_1, \dots ,p_t\}$
.
$p(\Gamma )=\mathrm {gcd}\{p_1, \dots ,p_t\}$
.
Proof Since
![]() $\Gamma _1,\dots ,\Gamma _t$
are strong, so is
$\Gamma _1,\dots ,\Gamma _t$
are strong, so is
![]() $\Gamma $
[Reference Hammack, Bang-Jensen and Gutin8, Theorem 10.3.2]. Since
$\Gamma $
[Reference Hammack, Bang-Jensen and Gutin8, Theorem 10.3.2]. Since
![]() $\Gamma _1,\dots ,\Gamma _t$
are digon-free and triangle-free, so is
$\Gamma _1,\dots ,\Gamma _t$
are digon-free and triangle-free, so is
![]() $\Gamma $
[Reference Zhang and Zhu18, Lemma 2.4].
$\Gamma $
[Reference Zhang and Zhu18, Lemma 2.4].
Let
![]() $r=\mathrm {gcd}\{p_1,\dots ,p_t\}$
and
$r=\mathrm {gcd}\{p_1,\dots ,p_t\}$
and
![]() $p=p(\Gamma )$
. Since every cycle of each
$p=p(\Gamma )$
. Since every cycle of each
![]() $\Gamma _i$
has a corresponding cycle in
$\Gamma _i$
has a corresponding cycle in
![]() $\Gamma $
, the lengths of the cycles in the
$\Gamma $
, the lengths of the cycles in the
![]() $\Gamma _i$
’s are lengths of cycles in
$\Gamma _i$
’s are lengths of cycles in
![]() $\Gamma $
, so p divides the lengths of all cycles in all
$\Gamma $
, so p divides the lengths of all cycles in all
![]() $\Gamma _i$
’s, so p divides the greatest common divisor of these lengths. That is, p divides r.
$\Gamma _i$
’s, so p divides the greatest common divisor of these lengths. That is, p divides r.
We shall say that an arc
![]() $[ (u_1,\dots , u_t) , (v_1,\dots , v_t)]\in A(\Gamma )$
is of type r if
$[ (u_1,\dots , u_t) , (v_1,\dots , v_t)]\in A(\Gamma )$
is of type r if
![]() $u_i=v_i$
for each
$u_i=v_i$
for each
![]() $1\leq i \leq t$
,
$1\leq i \leq t$
,
![]() $i\neq r$
. Consider a cycle of length l that involves
$i\neq r$
. Consider a cycle of length l that involves
![]() $l_r$
arcs of type r (
$l_r$
arcs of type r (
![]() $1\leq r\leq t$
). Then, for each
$1\leq r\leq t$
). Then, for each
![]() $1\leq i\leq t$
,
$1\leq i\leq t$
,
![]() $l_i\equiv 0 \bmod p_i$
and so
$l_i\equiv 0 \bmod p_i$
and so
![]() $l_i\equiv 0 \bmod r$
. Therefore,
$l_i\equiv 0 \bmod r$
. Therefore,
![]() $l=l_1+\cdots + l_t\equiv 0 \bmod r$
. Thus, r divides the length of any cycle in
$l=l_1+\cdots + l_t\equiv 0 \bmod r$
. Thus, r divides the length of any cycle in
![]() $\Gamma $
, so l divides the greatest common divisor of the lengths of the cycles in
$\Gamma $
, so l divides the greatest common divisor of the lengths of the cycles in
![]() $\Gamma $
. That is, r divides p, and hence
$\Gamma $
. That is, r divides p, and hence
![]() $r=p$
.
$r=p$
.
Example 5.6 (Cartesian product of cycles)
Let
![]() $\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
where
$\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
where
![]() $\Gamma _i$
(
$\Gamma _i$
(
![]() $1\leq i\leq t$
) is the cycle of length
$1\leq i\leq t$
) is the cycle of length
![]() $m_i\geq 4$
(
$m_i\geq 4$
(
![]() $1\leq i\leq t$
). Then
$1\leq i\leq t$
). Then
![]() $\Gamma $
is strong, digon-free, and triangle-free, with period
$\Gamma $
is strong, digon-free, and triangle-free, with period
![]() $\mathrm {gcd}\{ m_1,\dots , m_t\}$
. (Note that
$\mathrm {gcd}\{ m_1,\dots , m_t\}$
. (Note that
![]() $\Gamma $
is the Cayley digraph
$\Gamma $
is the Cayley digraph
![]() $\mathrm {Cay}(\mathbb {Z}_{m_1}\oplus \cdots \oplus \mathbb {Z}_{m_t},\{e_1,\dots ,e_t\})$
, where
$\mathrm {Cay}(\mathbb {Z}_{m_1}\oplus \cdots \oplus \mathbb {Z}_{m_t},\{e_1,\dots ,e_t\})$
, where
![]() $e_1=(1,0,\dots ,0), e_2=(0,1,0,\dots ,0), \dots , e_t=(0,0,\dots ,1)$
.)
$e_1=(1,0,\dots ,0), e_2=(0,1,0,\dots ,0), \dots , e_t=(0,0,\dots ,1)$
.)
Corollary 5.7 Let
![]() $\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
be the Cartesian product of digon-free and triangle-free, strong digraphs
$\Gamma =\Gamma _1 \square \dots \square \Gamma _t$
be the Cartesian product of digon-free and triangle-free, strong digraphs
![]() $\Gamma _1,\dots , \Gamma _t$
with periods
$\Gamma _1,\dots , \Gamma _t$
with periods
![]() $p_1,\dots , p_t$
, respectively, and let
$p_1,\dots , p_t$
, respectively, and let
![]() $p=\mathrm {gcd}\{p_1, \dots , p_t\}$
. Let
$p=\mathrm {gcd}\{p_1, \dots , p_t\}$
. Let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() $G=G_{\Gamma} (R)$
is finite if and only if
$G=G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha \neq 0, \beta \neq 0$
,
$\alpha \neq 0, \beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
,
$\alpha ^p\neq \beta ^p$
,
![]() $a^\alpha =b^\beta $
in K, in which case G is cyclic of order
$a^\alpha =b^\beta $
in K, in which case G is cyclic of order
![]() $|\alpha ^{p}-\beta ^{p}|$
.
$|\alpha ^{p}-\beta ^{p}|$
.
5.4 Direct products of strong digraphs
Lemma 5.8 Let
![]() $\Gamma =\Gamma _1 \times \dots \times \Gamma _t$
be the direct product of strong digraphs
$\Gamma =\Gamma _1 \times \dots \times \Gamma _t$
be the direct product of strong digraphs
![]() $\Gamma _1,\dots ,\Gamma _t$
with periods
$\Gamma _1,\dots ,\Gamma _t$
with periods
![]() $p_1,\dots ,p_t$
, respectively, where
$p_1,\dots ,p_t$
, respectively, where
![]() $\mathrm {gcd}\{p_1,\dots , p_t\}=1$
, and where at least one of
$\mathrm {gcd}\{p_1,\dots , p_t\}=1$
, and where at least one of
![]() $\Gamma _1,\dots ,\Gamma _t$
is digon-free and at least one is triangle-free. Then
$\Gamma _1,\dots ,\Gamma _t$
is digon-free and at least one is triangle-free. Then
![]() $\Gamma $
is strong, digon-free, and triangle-free, with period
$\Gamma $
is strong, digon-free, and triangle-free, with period
![]() $p(\Gamma )=p_1\cdots p_t$
.
$p(\Gamma )=p_1\cdots p_t$
.
Proof The digraph
![]() $\Gamma $
is strong with period
$\Gamma $
is strong with period
![]() $p(\Gamma )=p_1\cdots p_t$
by [Reference McAndrew14] (see [Reference McAndrew14, Theorem 1(ii) and (iii)] and page 251 and Proposition 4 of [Reference Harary and Trauth10]; see also [Reference Hammack, Bang-Jensen and Gutin8, Theorem 10.3.2]). If
$p(\Gamma )=p_1\cdots p_t$
by [Reference McAndrew14] (see [Reference McAndrew14, Theorem 1(ii) and (iii)] and page 251 and Proposition 4 of [Reference Harary and Trauth10]; see also [Reference Hammack, Bang-Jensen and Gutin8, Theorem 10.3.2]). If
![]() $\Gamma $
contains a digon (resp. triangle), then each of
$\Gamma $
contains a digon (resp. triangle), then each of
![]() $\Gamma _1,\dots , \Gamma _t$
contains a digon (resp. triangle), a contradiction. Hence,
$\Gamma _1,\dots , \Gamma _t$
contains a digon (resp. triangle), a contradiction. Hence,
![]() $\Gamma $
is digon-free and triangle-free.
$\Gamma $
is digon-free and triangle-free.
Example 5.9 (Direct product of an oriented diamond and a cycle)
Let
![]() $\Gamma = \Gamma _1\times \Gamma _2$
where
$\Gamma = \Gamma _1\times \Gamma _2$
where
![]() $\Gamma _1$
is the oriented diamond digraph with
$\Gamma _1$
is the oriented diamond digraph with
![]() $V(\Gamma _1)=\{u,v,w,t\}$
and
$V(\Gamma _1)=\{u,v,w,t\}$
and
![]() $A(\Gamma _1) = \{ [u,v], [u,w], [v,t], [w,t], [t,u] \}$
, and
$A(\Gamma _1) = \{ [u,v], [u,w], [v,t], [w,t], [t,u] \}$
, and
![]() $\Gamma _2$
is the cycle of length
$\Gamma _2$
is the cycle of length
![]() $n\geq 2$
where
$n\geq 2$
where
![]() $n \not \equiv 0 \bmod 3$
. Then
$n \not \equiv 0 \bmod 3$
. Then
![]() $\Gamma _1$
is strong and digon-free with period
$\Gamma _1$
is strong and digon-free with period
![]() $3$
and
$3$
and
![]() $\Gamma _2$
is strong and triangle-free with period n, so
$\Gamma _2$
is strong and triangle-free with period n, so
![]() $\Gamma $
is strong, digon-free, and triangle free, of period
$\Gamma $
is strong, digon-free, and triangle free, of period
![]() $p(\Gamma )=3n$
.
$p(\Gamma )=3n$
.
Corollary 5.10 Let
![]() $\Gamma =\Gamma _1 \times \dots \times \Gamma _t$
be the direct product of strong digraphs
$\Gamma =\Gamma _1 \times \dots \times \Gamma _t$
be the direct product of strong digraphs
![]() $\Gamma _1,\dots ,\Gamma _t$
with periods
$\Gamma _1,\dots ,\Gamma _t$
with periods
![]() $p_1,\dots ,p_t$
, respectively, where
$p_1,\dots ,p_t$
, respectively, where
![]() $\mathrm {gcd}\{p_1,\dots , p_t\}=1$
, and where at least one of
$\mathrm {gcd}\{p_1,\dots , p_t\}=1$
, and where at least one of
![]() $\Gamma _1,\dots ,\Gamma _t$
is digon-free and at least one is triangle-free, and let
$\Gamma _1,\dots ,\Gamma _t$
is digon-free and at least one is triangle-free, and let
![]() $p=p_1\cdots p_t$
. Let
$p=p_1\cdots p_t$
. Let
![]() $R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
$R(a,b)$
be a cyclically reduced word that involves both a and b and which has exponent sums
![]() $\alpha ,\beta $
in a and
$\alpha ,\beta $
in a and
![]() $b^{-1}$
, respectively, and let
$b^{-1}$
, respectively, and let
![]() $K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
$K=\langle {a,b}\ |\ {R(a,b)} \rangle $
. Then
![]() $G=G_{\Gamma} (R)$
is finite if and only if
$G=G_{\Gamma} (R)$
is finite if and only if
![]() $\alpha \neq 0$
,
$\alpha \neq 0$
,
![]() $\beta \neq 0$
,
$\beta \neq 0$
,
![]() $\mathrm {gcd}\{\alpha ,\beta \}=1$
,
$\mathrm {gcd}\{\alpha ,\beta \}=1$
,
![]() $\alpha ^p\neq \beta ^p$
,
$\alpha ^p\neq \beta ^p$
,
![]() $a^\alpha =b^\beta $
in K, in which case G is cyclic of order
$a^\alpha =b^\beta $
in K, in which case G is cyclic of order
![]() $|\alpha ^p-\beta ^p|$
.
$|\alpha ^p-\beta ^p|$
.
Acknowledgements
The authors thank David Penman for introducing them to the concept of the period of a digraph and for his insightful comments on a draft of this article.