Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nashed, M. Zuhair
1976.
Generalized Inverses and Applications.
p.
325.
Nashed, M.Z.
and
Rall, L.B.
1976.
Generalized Inverses and Applications.
p.
771.
Neuberger, J. W.
1983.
Ordinary Differential Equations and Operators.
Vol. 1032,
Issue. ,
p.
390.


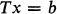
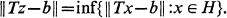 . It is easily shown that
. It is easily shown that 