Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-16T16:10:41.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Stackings and the W-cycles Conjecture

Published online by Cambridge University Press:  20 November 2018

Larsen Louder  and
Henry Wilton
Larsen Louder
Affiliation:
University College London, London, UK. e-mail: [email protected]
Henry Wilton
Affiliation:
University of Cambridge, Cambridge, UK. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

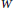We prove Wise's $W$-cycles conjecture. Consider a compact graph 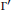$\Gamma '$ immersing into another graph $\Gamma $. For any immersed cycle 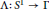$\Lambda :{{S}^{1}}\to \Gamma $, we consider the map 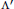$\Lambda '$ from the circular components $\mathbb{S}$ of the pullback to 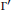$\Gamma '$. Unless 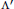$\Lambda '$ is reducible, the degree of the covering map 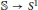$\mathbb{S}\to {{S}^{1}}$ is bounded above by minus the Euler characteristic of 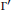$\Gamma '$. As a corollary, any finitely generated subgroup of a one-relator group has a finitely generated Schur multiplier.

Keywords

20F65free groupsone-relator groupsright-orderability
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 3 , 01 September 2017 , pp. 604 - 612
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Bau74] Baumslag, G., Some problems on one-relator groups. In: Proceedings of the Second International Conference on the Theory of Groups (Australian Nat. Univ., Canberra, 1973), Lecture Notes in Math., 372, Springer, Berlin, 1974, pp. 75–81. Google Scholar
[Bro80] Brodskii, S. D., Equations over groups and groups with one defining relation. Uspekhi Mat. Nauk 35(1980), no. 4(214), 183. Google Scholar
[DH91] Duncan, A. J. and J. Howie, The genus problem for one-relator products of locally indicable Google Scholar
groups. Math. Z. 208(1991), no. 2, 225–237. http://dx.doi.Org/10.1007/BF02571522 Google Scholar
[Far76] Farrell, E. T., Right-orderable deck transformation groups. Rocky Mountain J. Math. 6(1976), no. 3, 441–447. http://dx.doi.Org/10.1216/RMJ-1976-6-3-441 Google Scholar
[HW16] Heifer, J. and Wise, D. T., Counting cycles in labeled graphs: the nonpositive immersions property for one-relator groups. Int. Math. Res. Not. IMRN 2016, no. 9, 2813–2827. http://dx.doi.Org/10.1093/imrn/mv208 Google Scholar
[How81] Howie, J., On pairs of 2-complexes and systems of equations over groups. J. Reine Angew. Math. 324(1981), 165–174. http://dx.doi.Org/10.1 51 5/crll.1 981.324.1 65 Google Scholar
[How82] , On locally indicable groups. Math. Z. 180(1982), no. 4, 445–461. http://dx.doi.Org/10.1007/BF01 21471 7 Google Scholar
[Lyn50] Lyndon, R. C., Cohomology theory of groups with a single defining relation. Ann. of Math. (2) 52(1950), 650–665. http://dx.doi.Org/10.2307/1 969440 Google Scholar
[Sco73] Scott, G. P., Finitely generated 3-manifold groups are finitely presented. J. London Math. Soc. (2) 6(1973), 437–440. http://dx.doi.Org/10.1112/jlms/s2-6.3.437 Google Scholar
[Sta83] Stallings, J. R., Topology of finite graphs. Invent. Math. 71(1983), no. 3, 551–565. http://dx.doi.Org/10.1007/BF02095993 Google Scholar
[WisO5] Wise, D. T., The coherence of one-relator groups with torsion and the Hanna Neumann conjecture. Bull. London Math. Soc. 37(2005), no. 5, 697–705. http://dx.doi.Org/!0.1112/S0024609305004376 Google Scholar