Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-28T17:53:19.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable Components and Layers

Part of: Multivariate analysis Applied homological algebra and category theory Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  23 October 2019

J. F. Jardine
J. F. Jardine*
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Component graphs 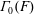$\unicode[STIX]{x1D6E4}_{0}(F)$ are defined for arrays of sets 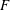$F$, and, in particular, for arrays of path components for Vietoris–Rips complexes and Lesnick complexes. The path components of 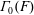$\unicode[STIX]{x1D6E4}_{0}(F)$ are the stable components of the array 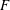$F$. The stable components for the system of Lesnick complexes 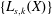$\{L_{s,k}(X)\}$ for a finite data set 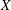$X$ decompose into layers, which are themselves path components of a graph. Combinatorial scoring functions are defined for layers and stable components.

Keywords

clustergraphstable componentlayer

MSC classification

Primary: 55U10: Simplicial sets and complexes
Secondary: 68R10: Graph theory (including graph drawing) 62H30: Classification and discrimination; cluster analysis
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 562 - 576
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was partially supported by the Natural Sciences and Engineering Research Council of Canada.

References

Blumberg, A. J. and Lesnick, M., Universality of the homotopy interleaving distance. 2017. arxiv:1705.01690.Google Scholar
Campello, R. J. G. B., Moulavi, D., Zimek, A., and Sander, J., Hierarchical density estimates for data clustering, visualization, and outlier detection.. ACM Transactions on Knowledge Discovery from Data (TKDD) 10(2016), 1–51. https://doi.org/10.1145/2733381CrossRefGoogle Scholar
Carlsson, G. and Memoli, F., Multiparameter hierarchical clustering methods. In: Classification as a tool for research. Stud. Classification Data Anal. Knowledge Organ, Springer, Berlin, 2010, pp. 63–70. https://doi.org/10.1007/978-3-642-10745-0_6CrossRefGoogle Scholar
Lesnick, M. and Wright, M., RIVET: visualization and analysis of two-dimensional persistent homology. 2019. http://rivet.online.Google Scholar
McInnes, L. and Healy, J., 2017 IEEE International Conference on Data Mining Workshops. (ICDM Workshops 2017, New Orleans, LA, USA (November 18–21)), IEEE, 2017, pp. 33–42. https://doi.org/10.1109/ICDMW.2017.12Google Scholar
Stuetzle, W., Estimating the cluster tree of a density by analyzing the minimal spanning tree of a sample. J. Classification 20(2003), 25–47. https://doi.org/10.1007/s00357-003-0004-6CrossRefGoogle Scholar
Zomorodian, A., Fast construction of the Vietoris-Rips complex. Computers & Graphics 34(2010), 263–271. https://doi.org/10.1016/j.cag.2010.03.007CrossRefGoogle Scholar