Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T16:06:47.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectrality of a Class of Moran Measures

Part of: Normed linear spaces and Banach spaces; Banach lattices Nontrigonometric harmonic analysis Classical measure theory

Published online by Cambridge University Press:  17 January 2020

Ming-Liang Chen ,
Jing-Cheng Liu ,
Juan Su  and
Xiang-Yang Wang
Ming-Liang Chen
Affiliation:
School of Mathematics, Sun Yat-Sen University, Guangzhou 510275, P.R. China Email: [email protected]@mail.sysu.edu.cn
Jing-Cheng Liu
Affiliation:
Key Laboratory of High Performance Computing and Stochastic Information Processing (Ministry of Education of China), College of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan 410081, P.R. China Email: [email protected]
Juan Su
Affiliation:
Changsha School of Mathematics and Statistics, University of Science & Technology, Changsha, Hunan 410114, P.R. China Email: [email protected]
Xiang-Yang Wang
Affiliation:
School of Mathematics, Sun Yat-Sen University, Guangzhou 510275, P.R. China Email: [email protected]@mail.sysu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 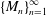$\{M_{n}\}_{n=1}^{\infty }$ be a sequence of expanding matrices with 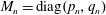$M_{n}=\operatorname{diag}(p_{n},q_{n})$, and let 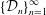$\{{\mathcal{D}}_{n}\}_{n=1}^{\infty }$ be a sequence of digit sets with 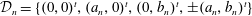${\mathcal{D}}_{n}=\{(0,0)^{t},(a_{n},0)^{t},(0,b_{n})^{t},\pm (a_{n},b_{n})^{t}\}$, where 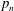$p_{n}$, 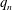$q_{n}$, 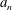$a_{n}$ and 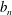$b_{n}$ are positive integers for all 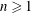$n\geqslant 1$. If 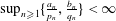$\sup _{n\geqslant 1}\{\frac{a_{n}}{p_{n}},\frac{b_{n}}{q_{n}}\}<\infty$, then the infinite convolution 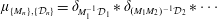$\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}}=\unicode[STIX]{x1D6FF}_{M_{1}^{-1}{\mathcal{D}}_{1}}\ast \unicode[STIX]{x1D6FF}_{(M_{1}M_{2})^{-1}{\mathcal{D}}_{2}}\ast \cdots \,$ is a Borel probability measure (Cantor–Dust–Moran measure). In this paper, we investigate whenever there exists a discrete set 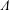$\unicode[STIX]{x1D6EC}$ such that 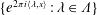$\{e^{2\unicode[STIX]{x1D70B}i\langle \unicode[STIX]{x1D706},x\rangle }:\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}\}$ is an orthonormal basis for 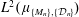$L^{2}(\unicode[STIX]{x1D707}_{\{M_{n}\},\{{\mathcal{D}}_{n}\}})$.

Keywords

Cantor–Dust–Moran measurespectral measurespectruminfinite convolution

MSC classification

Primary: 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 366 - 381
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is supported in part by the NNSF of China (Nos. 11401053, 11771457, 11571104 and 11971500) and the SRF of Hunan Provincial Education Department (Nos. 17B158 and 14C0046). Author X.-Y. W. is the corresponding author.

References

An, L. X. and He, X. G., A class of spectral Moran measures. J. Funct. Anal. 266(2014), 343–354.CrossRefGoogle Scholar
An, L. X., He, X. G., and Lau, K. S., Spectrality of a class of infinite convolutions. Adv. Math. 283(2015), 362–376.CrossRefGoogle Scholar
Dai, X. R., When does a Bernoulli convolution admit a spectrum? Adv. Math. 231(2012), 1681–1693.CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lai, C. K., Spectral property of Cantor measures with consecutive digits. Adv. Math. 242(2013), 187–208.CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lau, K. S., On spectral N-Bernoulli measures. Adv. Math. 259(2014), 511–531.CrossRefGoogle Scholar
Deng, Q. R. and Lau, K. S., Sierpinski-type spectral self-similar measures. J. Funct. Anal. 269(2015), 1310–1326.CrossRefGoogle Scholar
Deng, Q. R., On the spectra of Sierpinski-type self-affine measures. J. Funct. Anal. 270(2016), 4426–4442.CrossRefGoogle Scholar
Dutkay, D., Haussermann, J., and Lai, C. K., Hadamard triples generate self-affine spectral measures. Trans. Amer. Math. Soc. 371(2019), 1439–1481.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Analysis of orthogonality and of orbits in affine iterated function systems. Math. Z. 256(2007), 801–823.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Fourier frequencies in affine iterated function systems. J. Funct. Anal. 247(2007), 110–137.CrossRefGoogle Scholar
Fu, X. Y., He, X. G., and Lau, K. S., Spectrality of self-similar tiles. Constr. Approx. 45(2015), 519–541.CrossRefGoogle Scholar
Fu, Y. S. and Wen, Z. X., Spectral property of a class of Moran measures on ℝ. J. Math. Anal. Appl. 430(2015), 572–584.CrossRefGoogle Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem. J. Funct. Anal. 16(1974), 101–121.CrossRefGoogle Scholar
He, L. and He, X. G., On the Fourier orthonormal bases of Cantor–Moran measures. J. Funct. Anal. 272(2017), 1980–2004.CrossRefGoogle Scholar
Hutchinson, J., Fractals and self-similarity. Indiana Univ. Math. J. 30(1981), 713–747.CrossRefGoogle Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolutions. Adv. Math. 219(2008), 554–567.CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal L 2-spaces. J. Anal. Math. 75(1998), 185–228.CrossRefGoogle Scholar
Kolountzakis, M. and Matolcsi, M., Complex Hadamard matrices and the spectral set conjecture. Collect. Math. 57(2006), 281–291.Google Scholar
Kolountzakis, M. and Matolcsi, M., Tiles with no spectra. Forum Math. 18(2006), 519–528.CrossRefGoogle Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures. J. Funct. Anal. 193(2002), 409–420.CrossRefGoogle Scholar
Li, J. L., Non-spectral problem for a class of planar self-affine measures. J. Funct. Anal. 255(2008), 3125–3148.CrossRefGoogle Scholar
Li, J. L., Spectra of a class of self-affine measures. J. Funct. Anal. 260(2011), 1086–1095.CrossRefGoogle Scholar
Li, J. L., Spectrality of self-affine measures and generalized compatible pairs. Monatsh. Math. 184(2017), 611–625.CrossRefGoogle Scholar
Liu, J. C., Dong, X. H., and Li, J. L., Non-spectral problem for the self-affine measures. J. Funct. Anal. 273(2017), 705–720.CrossRefGoogle Scholar
Liu, J. C. and Luo, J. J., Spectral property of self-affine measures on ℝn. J. Funct. Anal. 272(2017), 599–612.CrossRefGoogle Scholar
Strichartz, R., Remarks on: “Dense analytic subspaces in fractal spaces” by P. Jorgensen and S. Pedersen. J. Anal. Math. 75(1998), 229–231.CrossRefGoogle Scholar
Strichartz, R., Mock Fourier series and transforms associated with certain Cantor measures. J. Anal. Math. 81(2000), 209–238.CrossRefGoogle Scholar
Tao, T., Fuglede’s conjecture is false in 5 and higher dimensions. Math. Res. Lett. 11(2004), 251–258.CrossRefGoogle Scholar
Tang, M. W. and Yin, F. L., Spectrality of Moran measures with four-element digit sets. J. Math. Anal. Appl. 461(2018), 354–363.CrossRefGoogle Scholar
Wang, Z. Y., Dong, X. H., and Liu, Z. S., Spectrality of certain Moran measures with three-element digit sets. J. Math. Anal. Appl. 459(2018), 743–752.CrossRefGoogle Scholar